
科目: 来源: 题型:
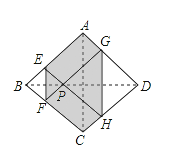
【题目】如图,正方形纸片![]() 的边长为
的边长为![]() ,翻折
,翻折![]() ,使两个直角顶点重合于对角线
,使两个直角顶点重合于对角线![]() 上一点
上一点![]() 分别是折痕,设
分别是折痕,设![]() ,给出下列判断:
,给出下列判断:
①当![]() 时,点
时,点![]() 是正方形
是正方形![]() 的中心;
的中心;
②当![]() 时,
时,![]() ;
;
③当![]() 时,六边形
时,六边形![]() 面积的最大值是
面积的最大值是![]()
④当![]() 时,六边形
时,六边形![]() 周长的值不变.
周长的值不变.
其中错误的是( )
A.②③B.③④C.①④D.①②
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )

A.线段BEB.线段EFC.线段CED.线段DE
查看答案和解析>>
科目: 来源: 题型:
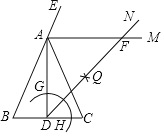
【题目】如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于![]() GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则△ADF的形状是( )
GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则△ADF的形状是( )
A.等腰三角形B.等边三角形
C.直角三角形D.等腰直角三角形
查看答案和解析>>
科目: 来源: 题型:
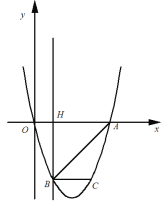
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,-3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)点P是抛物线上一动点,当ΔABP的面积为3时,求出点P的坐标;
(3)若点M在直线BH上运动,点N在x轴上运动,点R是坐标平面内一点,当以点C、M、N、R为顶点的四边形为正方形时,请直接写出此时点R的坐标.
查看答案和解析>>
科目: 来源: 题型:
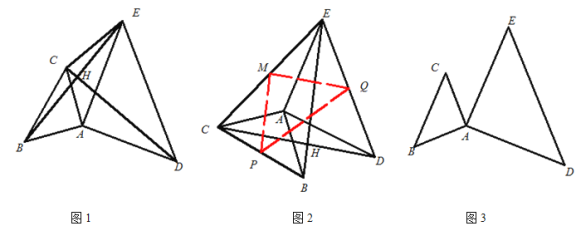
【题目】已知:△ABC和△ADE是两个不全等的等腰直角三角形,其中AB=AC,AD=AE,
∠BAC=90°,∠DAE=90°.
(1)观察猜想
如图1,连接BE、CD交于点H,再连接CE,那么BE和CD的数量关系和位置关系分别是
(2)探究证明
将图1中的△ABC绕点A逆时针旋转到图2的位置时,分别取BC、CE、DE的中点P、M、Q,连接MP、PQ、MQ,请判断MP和MQ的数量关系和位置关系,并说明理由;
(3)拓展延伸
已知AB=![]() ,AD=4,在(2)的条件下,将△ABC绕点A旅转的过程中,若∠CAE=45°,请直接写出此时线段PQ的长.
,AD=4,在(2)的条件下,将△ABC绕点A旅转的过程中,若∠CAE=45°,请直接写出此时线段PQ的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某宝网店销售甲、乙两种电器,已知甲种电器每个的售价比乙种电器多60元,马老师从该网店购买了3个甲种电器和2个乙种电器,共花费780元.
(1)该店甲、乙两种电器每个的售价各是多少元?
(2)根据销售情况,店主决定用不少于10800元的资金购进甲、乙两种电器,这两种电器共100个,已知甲种电器每个的进价为150元,乙种电器每个的进价为80元.若所购进电器均可全部售出,请求出网店所获利润W(元)与甲种电器进货量m(个)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】在学习函数时,我们经历了“确定函数的表达式利用函数图象研究其性质——运用函数解决问题“的学习过程,在画函数图象时,我们通过列表、描点、连线的方法画出了所学的函数图象
同时,我们也学习过绝对值的意义![]() .
.
结合上面经历的学习过程,现在来解决下面的问题:
在函数y=|kx-1|+b中,当x=0时,y=-2;当x=1时,y=-3.
(1)求这个函数的表达式;
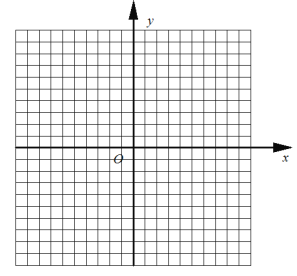
(2)在给出的平面直角坐标系中,请直接画出此函数的图象并写出这个函数的两条性质;
(3)在图中作出函数y=![]() 的图象,结合你所画的函数图象,直接写出不等式|kx-1|+b≤
的图象,结合你所画的函数图象,直接写出不等式|kx-1|+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.4cm,CD=8cm,AB=40cm,BC=45cm,
 图1
图1
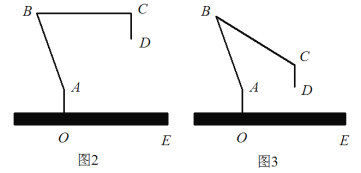
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO= °
②投影探头的端点D到桌面OE的距离
(2)如图3,将(1)中的BC向下旋转,∠ABC=30°时,求投影探头的端点D到桌面OE的距离
(参考数据:sin70≈0.94,cos70≈0.34,sin40°≈0.64,cos40°≈0.77)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC,BC交于点E,F. 过点F作⊙O的切线交AB于点M.

(1)求证:MF⊥AB;
(2)若⊙O的直径是6,填空:
①连接OF,OM,当FM= 时,四边形OMBF是平行四边形;
②连接DE,DF,当AC= 时,四边形CEDF是正方形.
查看答案和解析>>
科目: 来源: 题型:
【题目】期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
(收集数据)
(1)若要从全年级学生中抽取一个48人的样本,你认为以下抽样方法中比较合理的有 ;(只要填写序号即可)
①随机抽取一个班级的48名学生;②在全年级学生中随机抽取48名学生;③在全年级12个班中分别各抽取4名学生;④从全年级学生中随机抽取48名男生;
(整理数据)
(2)将抽取的48名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图(不完整)如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 、
②估计全年级A、B类学生大约一共有 名;

成绩(分) | 频数 | 频率 |
A类(80~100) | 0.5 | |
B类(60~79) | 0.25 | |
C类(40~59) | 8 | |
D类(0~39) | 4 |
(3)学校为了解其他学校教学情况,将同层次的第一、第二两所中学的抽样数据进行对比,得下表:
学校 | 平均分(分) | 极差(分) | 方差 | A、B类的频率和 |
第一中学 | 71 | 52 | 432 | 0.75 |
第二中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校的教学效果较好?结合数据,请给出一个解释来支持你的观点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com