
科目: 来源: 题型:
【题目】一个智力挑战赛需要全部答对两道单项选择题,才能顺利通过第一关.第一道题有![]() 个选项,第二道题有
个选项,第二道题有![]() 个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
(1)如果小新在第--题使用“求助卡”,请用树状图或者列表来分析小新顺利通过第一关的概率;
(2)从概率的角度分析,你建议小新在第几题使用“求助卡”.为什么.
查看答案和解析>>
科目: 来源: 题型:
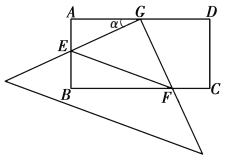
【题目】在矩形![]() 中,
中,![]() 为
为![]() 的中点,一块足够大的三角板的直角顶点与点
的中点,一块足够大的三角板的直角顶点与点![]() 重合,将三角板绕点
重合,将三角板绕点![]() 旋转,三角板的两直角边分别交
旋转,三角板的两直角边分别交![]() 或它们的延长线)于点
或它们的延长线)于点![]() ,设
,设![]() ,下列四个结论:①
,下列四个结论:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() ,正确的个数是( )
,正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,P是AB边上的任意一点,过P点作PE⊥AB,交AD于E,连结CE、CP.已知∠A=60o .
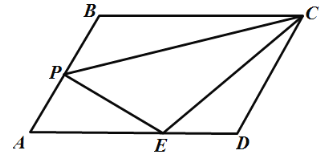
(1)试探究,当△CPE≌△CPB时,CD与DE的数量关系;
(2)若BC=4,AB=3,当AP的长为多少时,△CPE的面积最大,并求出面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并解答后面的问题.
在学习了直角三角形的边角关系后,小颖和小明两个学习小组继续探究任意锐角三角形的边角关系:在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.
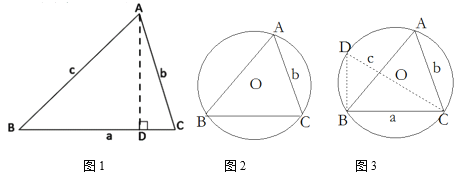
(1)小明学习小组发现如下结论:
如图1,过A作AD⊥BC于D,则sinB=![]() ,sinC=
,sinC=![]() 即AD=csinB,AD=bsinC,于是_____=______即
即AD=csinB,AD=bsinC,于是_____=______即![]() ,同理有
,同理有![]() ,
,![]()
则有![]()
(2)小颖学习小组则利用圆的有关性质也得到了类似的结论:
如图2,△ABC的外接圆半径为R,连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,
∵CD为⊙O的直径,∴∠DBC=90°,
在Rt△DBC中,
∵![]() ,
,
∴![]() ,
,![]()
同理:![]() ,
,
则有![]()
请你将这一结论用文字语言描述出来: .
小颖学习小组在证明过程中略去了“![]() ”的证明过程,请你把“
”的证明过程,请你把“![]() ”的证明过程补写出来.
”的证明过程补写出来.
(3)直接用前面阅读材料中得出的结论解决问题
规划局为了方便居民,计划在三个住宅小区A、B、C之间修建一座学校,使它到三个住宅小区的距离相等,已知小区C在小区B的正东方向![]() 千米处,小区A在小区B的东北方向,且A与C之间相距
千米处,小区A在小区B的东北方向,且A与C之间相距![]() 千米,求学校到三个小区的距离及小区A在小区C的什么方向?
千米,求学校到三个小区的距离及小区A在小区C的什么方向?
查看答案和解析>>
科目: 来源: 题型:
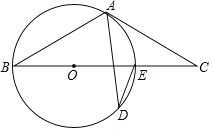
【题目】如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点.
(1)若∠ADE=25°,求∠C的度数;
(2)若AB=AC,CE=2,求⊙O半径的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目: 来源: 题型:
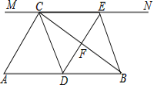
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上中点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:DF=![]() AC
AC
(2)试判断四边形BECD是什么特殊四边形?说明你的理由;
查看答案和解析>>
科目: 来源: 题型:
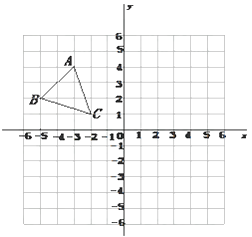
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
查看答案和解析>>
科目: 来源: 题型:
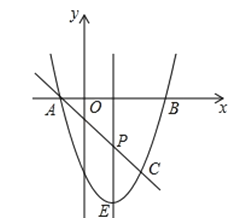
【题目】如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点(A点在B点左侧),A(﹣1,0),B(3,0),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
(1)求抛物线的函数解析式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A,C,F,G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com