
科目: 来源: 题型:
【题目】某市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第Ⅰ级:居民每户每月用水不超过18吨时,每吨收水费3元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过的部分每吨收水费4元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第Ⅰ、Ⅱ级标准收费,超过的部分每吨收水费6元.
现把上述水费阶梯收费办法称为方案①;假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费.
设一户居民月用水x吨.
(Ⅰ)根据题意填表:

(Ⅱ)设方案①应缴水费为![]() 元,方案②应缴水费为
元,方案②应缴水费为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)当![]() 时,通过计算说明居民选择哪种付费方式更合算.
时,通过计算说明居民选择哪种付费方式更合算.
查看答案和解析>>
科目: 来源: 题型:
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于G,过C点的切线与射线
于G,过C点的切线与射线![]() 相交于点E,直线
相交于点E,直线![]() 与
与![]() 交于点H,
交于点H,![]() ,
,![]() .
.

(Ⅰ)求![]() 的半径;
的半径;
(Ⅱ)将射线![]() 绕D点逆时针旋转,得射线
绕D点逆时针旋转,得射线![]() (如图2),
(如图2),![]() 与
与![]() 交于点M,与
交于点M,与![]() 及切线
及切线![]() 分别相交于点N,F,当
分别相交于点N,F,当![]() 时,求切线
时,求切线![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校350名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成了图1和图2两个统计图表.
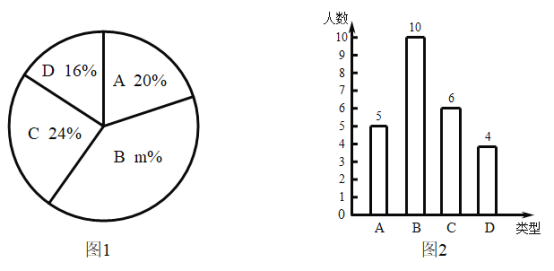
请根据相关信息回答下列问题:
(Ⅰ)此次共随机抽查了_______________名学生每人的植树量;
图①中m的值为_______________________;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计这350名学生共植树多少棵?
查看答案和解析>>
科目: 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得______________________;
(Ⅱ)解不等式②,得____________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为_______________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,A,B,D,E为格点,C为![]() ,
,![]() 的延长线的交点.
的延长线的交点.
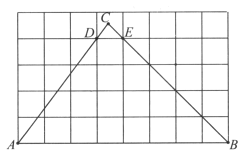
(Ⅰ)![]() 的结果为_________________.
的结果为_________________.
(Ⅱ)若点R在线段![]() 上,点S在线段
上,点S在线段![]() 上,点T在线段
上,点T在线段![]() 上,且满足四边形
上,且满足四边形![]() 为菱形,请在如图所示的网格中,用无刻度的直尺,画出菱形
为菱形,请在如图所示的网格中,用无刻度的直尺,画出菱形![]() ,并简要说明点R,S,T的位置是如何找到的(不要求证明)____________________.
,并简要说明点R,S,T的位置是如何找到的(不要求证明)____________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为_____.
经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为_____.
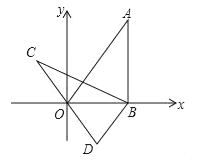
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,其中
,其中![]() .
.
(1)以下结论正确的序号有_________;
①抛物线的对称轴是直线![]() ; ②抛物线经过定点
; ②抛物线经过定点![]() ,
,![]() ;
;
③函数![]() 随着
随着![]() 的增大而减小; ④抛物线的顶点坐标为
的增大而减小; ④抛物线的顶点坐标为![]() .
.
(2)将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() .
.
①若抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,求抛物线
轴对称,求抛物线![]() 的解析式;
的解析式;
②抛物线![]() 顶点的纵坐标
顶点的纵坐标![]() 与横坐标
与横坐标![]() 之间存在一个函数关系,求这个函数关系式,并写出
之间存在一个函数关系,求这个函数关系式,并写出![]() 的取值范围;
的取值范围;
③若抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ,求
,求![]() 间的最小距离.
间的最小距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com