
科目: 来源: 题型:
【题目】如图1所示的健身器械为倒蹬机,使用方法为上身不动,腿部向前发力,双腿伸直之后,然后再慢慢回收.图2为示意图,已知![]() 在初始位置,
在初始位置,![]() , 点
, 点![]() 在同一直线上,
在同一直线上,![]() .
.

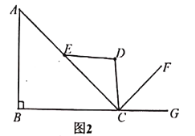
(1)当![]() 在初始位置时,求点
在初始位置时,求点![]() 到
到![]() 的距离;
的距离;
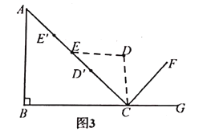
(2)当双腿伸直后,如图3,点![]() 分别从初始位置运动到点
分别从初始位置运动到点![]() , 假设
, 假设![]() 三点共线,求此时点
三点共线,求此时点![]() 上升的竖直高度. ( 结果精确到个位) (参考数据:
上升的竖直高度. ( 结果精确到个位) (参考数据:![]()
![]()
![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市购进一批成本为每件![]() 元的商品,经调查发现,该商品每天的销售量
元的商品,经调查发现,该商品每天的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间满足一次函数关系,其图象如图所示.
(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量![]() 与销售单价
与销售单价![]() 之间的函数关系式;
之间的函数关系式;
(2)若超市按单价不低于成本价,且不高于![]() 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润
元销售,则销售单价定为多少,才能使销售该商品每天获得的利润![]() (元)最大?
(元)最大?
(3)若超市要使销售该商品每天获得的利润为![]() 元,则每天的销售量应为多少件?
元,则每天的销售量应为多少件?
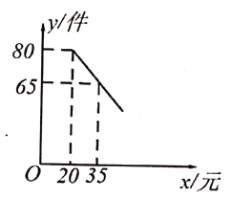
查看答案和解析>>
科目: 来源: 题型:
【题目】将一大、一小两个等腰直角三角形拼在一起,![]() ,连接
,连接![]() .
.
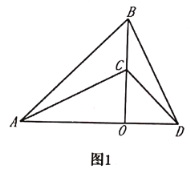
(1)如图1,若![]() 三点在同一条直线上,则
三点在同一条直线上,则![]() 与
与![]() 的关系是 ;
的关系是 ;
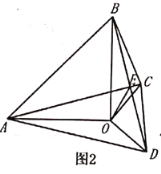
(2)如图2,若![]() 三点不在同一条直线上,
三点不在同一条直线上,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,猜想
,猜想![]() 之间的数量关系,并给予证明;
之间的数量关系,并给予证明;
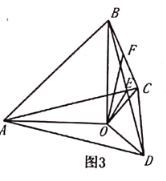
(3)如图3,在(2)的条件下作![]() 的中点
的中点![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 与
与![]() 之间的关系.
之间的关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,正方形![]() .... 按如图的方式放置.点
.... 按如图的方式放置.点![]()
![]() 和点
和点![]() 分别落在直线
分别落在直线![]() 和
和![]() 轴上.抛物线
轴上.抛物线![]() 过点
过点![]() ,且顶点在直线
,且顶点在直线![]() 上,抛物线
上,抛物线![]() 过点
过点![]() ,且顶点在直线
,且顶点在直线![]() 上,...按此规律,抛物线
上,...按此规律,抛物线![]() ,过点
,过点![]() , 且顶点也在直线
, 且顶点也在直线![]() 上,其中抛物线
上,其中抛物线![]() 交正方形
交正方形![]() 的边
的边![]() 于点
于点![]() ,抛物线
,抛物线![]() 交正方形
交正方形![]() 的边
的边![]() 于点
于点![]() (其中
(其中![]() 且
且![]() 为正整数) .
为正整数) .

(1)直接写出下列点的坐标:![]() ,
,![]() ;
;
(2)写出抛物线![]() 的解析式,并写出抛物线
的解析式,并写出抛物线![]() 的解析式求解过程,再猜想抛物线
的解析式求解过程,再猜想抛物线![]() 的顶点坐标;
的顶点坐标;
(3)设![]() ,试判断
,试判断![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
查看答案和解析>>
科目: 来源: 题型:
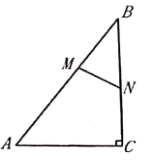
【题目】如图,在![]() 中,
中,![]() 动点
动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,运动时间为
匀速运动,运动时间为![]() 秒
秒![]() ,连接
,连接![]() .若以
.若以![]() 为直径的
为直径的![]() 与
与![]() 的边相切,则
的边相切,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目: 来源: 题型:
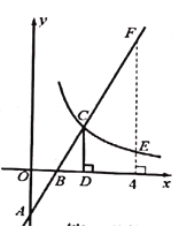
【题目】如图,在平面直角坐标系中,直线![]() 与坐标轴交于
与坐标轴交于![]() 两点,与双曲线
两点,与双曲线![]() 交于点
交于点![]() , 过点
, 过点![]() 作
作![]() 轴,且
轴,且![]() ,则以下结论错误的是( )
,则以下结论错误的是( )
A.![]()
B.当![]() 时,
时,![]()
C.当![]() 时,
时,![]()
D.当![]() 时,
时,![]() 随
随![]() 的增大而增大,
的增大而增大,![]() 随
随![]() 的增大而减小
的增大而减小
查看答案和解析>>
科目: 来源: 题型:
【题目】在“书香校园”活动中,学习委员对本班所有学生一周阅读时间(单位:小时)进行了统计,绘制了统计图,如图所示,根据统计图提供的信息,下列推断正确的是( )
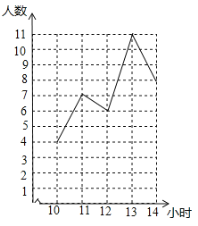
A.该班学生一周阅读时间为![]() 小时的有
小时的有![]() 人B.该班学生一周阅读时间的众数是
人B.该班学生一周阅读时间的众数是![]()
C.该班学生共有![]() 人D.该班学生一周阅读时间的中位数是
人D.该班学生一周阅读时间的中位数是![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以每秒1个单位长度的速度运动,动点
以每秒1个单位长度的速度运动,动点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以每秒2个单位长度的速度运动,过点
以每秒2个单位长度的速度运动,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .点
.点![]() 分别从点
分别从点![]() 同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为
同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为![]() 秒
秒![]() .
.
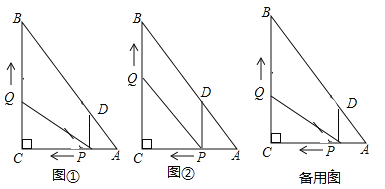
(1)如图①,直接用含![]() 的代数式分别表示:
的代数式分别表示:![]() ,
,![]() ______,
______,
(2)如图②,
①当![]() _____秒时,四边形
_____秒时,四边形![]() 为平行四边形.
为平行四边形.
②是否存在![]() 的值,使四边形
的值,使四边形![]() 为菱形?若存在,写出
为菱形?若存在,写出![]() 的值;若不存在,请求出当点
的值;若不存在,请求出当点![]() 的速度(匀速运动)变为每秒多少个单位长度时,才能使四边形
的速度(匀速运动)变为每秒多少个单位长度时,才能使四边形![]() 在某一时刻成为菱形?
在某一时刻成为菱形?
(3)设![]() 的外接圆面积为
的外接圆面积为![]() ,求出
,求出![]() 与
与![]() 的函数关系式,并判断当
的函数关系式,并判断当![]() 最小时,
最小时,![]() 的外接圆与直线
的外接圆与直线![]() 的位置关系,并且说明理由.
的位置关系,并且说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们规定,以二次函数![]() 的二次项系数
的二次项系数![]() 的2倍为一次项系数,一次项系数
的2倍为一次项系数,一次项系数![]() 为常数项构造的一次函数
为常数项构造的一次函数![]() 叫做二次函数
叫做二次函数![]() 的“子函数”,反过来,二次函数
的“子函数”,反过来,二次函数![]() 叫做一次函数
叫做一次函数![]() 的“母函数”.
的“母函数”.
(1)若一次函数![]() 是二次函数
是二次函数![]() 的“子函数”,且二次函数经过点
的“子函数”,且二次函数经过点![]() ,求此二次函数的解析式.
,求此二次函数的解析式.
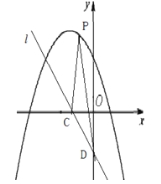
(2)如图,已知二次函数![]() 的“子函数”图象直线
的“子函数”图象直线![]() 与
与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 是直线
是直线![]() 上方的抛物线上任意一点,求
上方的抛物线上任意一点,求![]() 的面积的最大值.
的面积的最大值.
(3)已知二次函数![]() 与它的“子函数”
与它的“子函数”![]() 的函数图象有两个交点
的函数图象有两个交点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
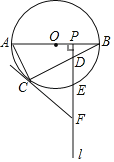
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,试证明四边形
,试证明四边形![]() 为菱形;
为菱形;
②若![]() ,且
,且![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com