
科目: 来源: 题型:
【题目】已知抛物线的顶点![]() ,经过点
,经过点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求该抛物线的解析式;
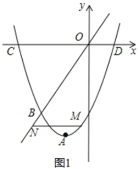
(2)如图1,点![]() 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线![]() 的下方,过点
的下方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,当
,当![]() 取最大值时,求点
取最大值时,求点![]() 的坐标;
的坐标;
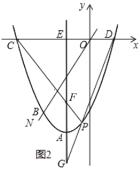
(3)如图2,![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 之间的一个动点,直线
之间的一个动点,直线![]() ,
,![]() 与
与![]() 分别交于
分别交于![]() ,
,![]() ,当点
,当点![]() 运动时.
运动时.
①直接写出![]() 的值;
的值;
②直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
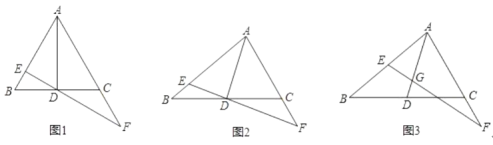
【题目】![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上(点
上(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 的直线交
的直线交![]() 于
于![]() ,交射线
,交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
(1)如图1,若![]() 为等边三角形,点
为等边三角形,点![]() 与
与![]() 重合,
重合,![]() ,求证:
,求证:![]() ;
;
(2)如图2,若点![]() 与
与![]() 重合,求证:
重合,求证:![]() ;
;
(3)如图3,若![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元.
(1)售价为![]() 元,月销量为
元,月销量为![]() 件;
件;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若销售该运动服的月利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求月利润最大时的售价;
的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了![]() 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则
元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目: 来源: 题型:
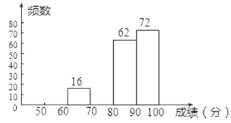
【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.
查看答案和解析>>
科目: 来源: 题型:
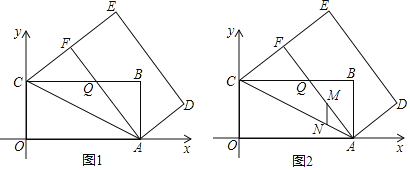
【题目】如图,反比例函数![]() 的图象分别与矩形
的图象分别与矩形![]() 的边
的边![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,与对角线
,与对角线![]() 交于点
交于点![]() ,以下结论:
,以下结论:
①若![]() 与
与![]() 的面积和为2,则
的面积和为2,则![]() ;
;
②若![]() 点坐标为
点坐标为![]() ,
,![]() ,则
,则![]() ;
;
③图中一定有![]() ;
;
④若点![]() 是
是![]() 的中点,且
的中点,且![]() ,则四边形
,则四边形![]() 的面积为18.
的面积为18.
其中一定正确个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
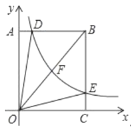
【题目】探索应用
材料一:如图1,在△ABC中,AB=c,BC=a,∠B=θ,用c和θ表示BC边上的高为 ,用a.c和θ表示△ABC的面积为 .
材料二:如图2,已知∠C=∠P,求证:CFBF=QFPF.
材料三:蝴蝶定理(ButterflyTheorem)是古代欧氏平面几何中最精彩的结果之一,最早出现在1815年,由W.G.霍纳提出证明,定理的图形象一只蝴蝶.
定理:如图3,M为弦PQ的中点,过M作弦AB和CD,连结AD和BC交PQ分别于点E和F,则ME=MF.
证明:设∠A=∠C=α,∠B=∠D=β,
∠DMP=∠CMQ=γ,∠AMP=∠BMQ=ρ,
PM=MQ=a,ME=x,MF=y
由![]()
即![]()
化简得:MF2AEED=ME2CFFB
则有:![]() ,
,
又∵CFFB=QFFP,AEED=PEEQ,
∴![]() ,即
,即![]()
即![]() ,从而x=y,ME=MF.
,从而x=y,ME=MF.
请运用蝴蝶定理的证明方法解决下面的问题:
如图4,B、C为线段PQ上的两点,且BP=CQ,A为PQ外一动点,且满足∠BAP=∠CAQ,判断△PAQ的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
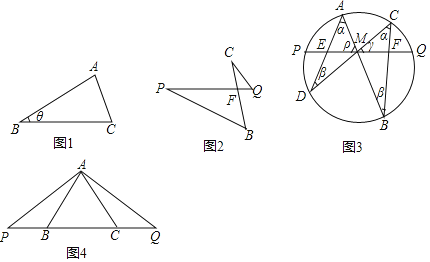
【题目】如图1,矩形OABC的顶点O是直角坐标系的原点,点A、C分别在x轴、y轴上,点B的坐标为(8,4),将矩形OABC绕点A顺时针旋转得到矩形ADEF,D、E、F分别与B、C、O对应,EF的延长线恰好经过点C,AF与BC相交于点Q.
(1)证明:△ACQ是等腰三角形;
(2)求点D的坐标;
(3)如图2,动点M从点A出发在折线AFC上运动(不与A、C重合),经过的路程为x,过点M作AO的垂线交AC于点N,记线段MN在运动过程中扫过的面积为S;求S关于x的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,以BC为直径作半圆O,以点D为圆心、DA为半径做圆弧交半圆O于点P.连结DP并延长交AB于点E.
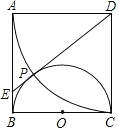
(1)求证:DE为半圆O的切线;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形构成.长方形的长为16m,宽为6m,抛物线的最高点C离路面AA1的距离为8m.
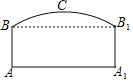
(1)建立适当的坐标系,求出表示抛物线的函数表达式;
(2)一大型货车装载设备后高为7m,宽为4m.如果隧道内设双向行驶车道,那么这辆货车能否安全通过?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com