
科目: 来源: 题型:
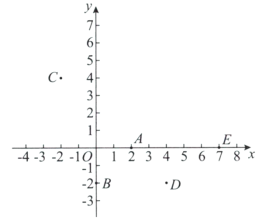
【题目】如图,在平面直角坐标系![]() 中,有五个点
中,有五个点![]() ,将二次函数
,将二次函数![]() 的图象记为W.下列的判断中
的图象记为W.下列的判断中
①点A一定不在W上;
②点B,C,D可以同时在W上;
③点C,E不可能同时在W上.
所有正确结论的序号是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】疫情期间某校学生积极观看网络直播课程,为了了解全校500名学生观看网络直播课程的情况,随机抽取50名学生,对他们观看网络直播课程的节数进行收集,并对数据进行了整理、描述和分析,下面给出了部分信息.
观看直播课节数的频数分布表
节数x | 频数 | 频率 |
| 8 | 0.16 |
| 10 | 0.20 |
| 16 |
|
|
| 0.24 |
| 4 | 0.08 |
总数 | 50 | 1 |

其中,节数在![]() 这一组的数据是:
这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)![]() __________,
__________,![]() __________
__________
(2)请补全频数分布直方图;
(3)随机抽取的50名学生观看直播课节数的中位数是___________;
(4)请估计该校学生中观看网络直播课节数不低于30次的约有__________人.
查看答案和解析>>
科目: 来源: 题型:
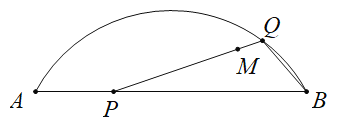
【题目】如图,M是弦![]() 与弧
与弧![]() 所围成的图形的内部的一个定点,P是弦
所围成的图形的内部的一个定点,P是弦![]() 上一动点,连接
上一动点,连接![]() 并延长交弧
并延长交弧![]() 于点Q,连接
于点Q,连接![]() .
.
已知![]() ,设A,P两点间的距离为
,设A,P两点间的距离为![]() ,P,Q两点间距离为
,P,Q两点间距离为![]() ,
,![]() 两点间距离为
两点间距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了![]() 与x的几组对应值,补全下表:
与x的几组对应值,补全下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 5.24 | 4.24 | 3.24 | 1.54 | 1.79 | 3.47 | |
| 1.31 | 1.34 | 1.42 | 1.54 | 1.80 | 2.45 | 3.47 |
(2)在同一平面直角坐标系![]() 中,描出表中各组数值对应的点
中,描出表中各组数值对应的点![]() 和
和![]() 并画出函数
并画出函数![]() 的图象;
的图象;
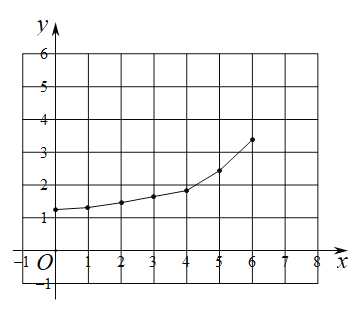
(3)结合函数图象,解决问题:当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约_________
的长度约_________![]() .(精确到0.1)
.(精确到0.1)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴的交点为A,B,与y轴交于C.
与x轴的交点为A,B,与y轴交于C.
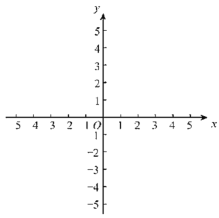
(1)求抛物线的对称轴和点C坐标;
(2)横、纵坐标都是整数的点叫做整点.拋物线在点A,B之间的部分与线段![]() 所围成的区域为图形W(不含边界).
所围成的区域为图形W(不含边界).
①当![]() 时,求图形W内的整点个数;
时,求图形W内的整点个数;
②若图形W内有2个整数点,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,延长
,延长![]() 使
使![]() ,线段
,线段![]() 绕点C顺时针旋转90°得到线段
绕点C顺时针旋转90°得到线段![]() ,连结
,连结![]() .
.
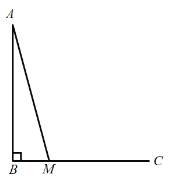
(1)依据题意补全图形;
(2)当![]() 时,
时,![]() 的度数是__________;
的度数是__________;
(3)小聪通过画图、测量发现,当![]() 是一定度数时,
是一定度数时,![]() .
.
小聪把这个猜想和同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:通过观察图形可以发现,如果把梯形![]() 补全成为正方形
补全成为正方形![]() ,就易证
,就易证![]() ,因此易得当
,因此易得当![]() 是特殊值时,问题得证;
是特殊值时,问题得证;
想法2:要证![]() ,通过第(2)问,可知只需要证明
,通过第(2)问,可知只需要证明![]() 是等边三角形,通过构造平行四边形
是等边三角形,通过构造平行四边形![]() ,易证
,易证![]() ,通过
,通过![]() ,易证
,易证![]() ,从而解决问题;
,从而解决问题;
想法3:通过![]() ,连结
,连结![]() ,易证
,易证![]() ,易得
,易得![]() 是等腰三角形,因此当
是等腰三角形,因此当![]() 是特殊值时,问题得证.
是特殊值时,问题得证.
请你参考上面的想法,帮助小聪证明当![]() 是一定度数时,
是一定度数时,![]() .(一种方法即可)
.(一种方法即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,点P是平面内任意一点,点A,B是![]() 上不重合的两个点,连结
上不重合的两个点,连结![]() .当
.当![]() 时,我们称点P为
时,我们称点P为![]() 的“关于
的“关于![]() 的关联点”.
的关联点”.

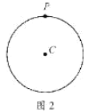
(1)如图2,当点P在![]() 上时,点P是
上时,点P是![]() 的“关于
的“关于![]() 的关联点”时,画出一个满足条件的
的关联点”时,画出一个满足条件的![]() ,并直接写出
,并直接写出![]() 的度数;
的度数;
(2)在平面直角坐标系中有点![]() ,点M关于y轴的对称点为点N.
,点M关于y轴的对称点为点N.
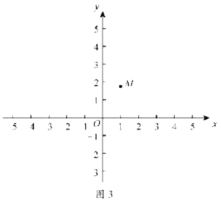
①以点O为圆心,![]() 为半径画
为半径画![]() ,在y轴上存在一点P,使点P为
,在y轴上存在一点P,使点P为![]() “关于
“关于![]() 的关联点”,直接写出点P的坐标;
的关联点”,直接写出点P的坐标;
②点![]() 是x轴上一动点,当
是x轴上一动点,当![]() 的半径为1时,线段
的半径为1时,线段![]() 上至少存在一点是
上至少存在一点是![]() 的“关于某两个点的关联点”,求m的取值范围.
的“关于某两个点的关联点”,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 的边长为2,函数
的边长为2,函数![]() 的图象经过点B,与直线
的图象经过点B,与直线![]() 交于点D.
交于点D.
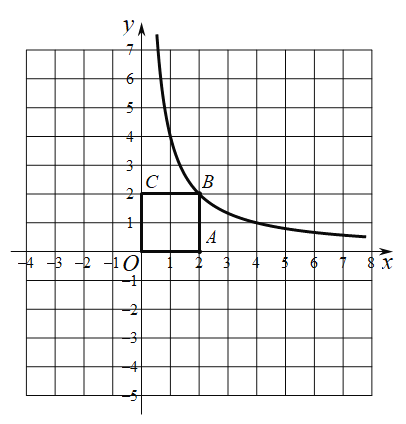
(1)求k的值;
(2)直线![]() 与
与![]() 边所在直线交于点M,与x轴交于点N.
边所在直线交于点M,与x轴交于点N.
①当点D为![]() 中点时,求b的值;
中点时,求b的值;
②当![]() 时,结合函数图象,直接写出b的取值范围.
时,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小元设计的“过直线外一点作已知直线的平行线”的尺规作图过程.

已知:如图,直线l和直线外一点P.
求作:过点P作直线l的平行线.
作法:如图,
①在直线l上任取点O;
②作直线![]() ;
;
③以点O为圆心![]() 长为半径画圆,交直线
长为半径画圆,交直线![]() 于点A,交直线l于点B;
于点A,交直线l于点B;
④连接![]() ,以点B为圆心,
,以点B为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 于点C(点A与C不重合);
于点C(点A与C不重合);
⑤作直线![]() .
.
则直线![]() 即为所求.
即为所求.
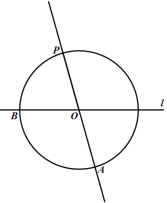
根据小元设计的尺规作图过程,完成以下任务.
(1)补全图形;
(2)完成下面的证明:
证明:连接![]()
∵![]()
∴![]()
∴![]() _______
_______![]() _________,
_________,
又∵![]() ,
,
∴![]() _______
_______![]() _________,
_________,
∴![]() ,
,
∴![]() (___________________________)(填推理的依据).
(___________________________)(填推理的依据).
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场在端午节前以1元/个的价格购进1000个粽子,现有以下三种销售方式:不加工直接卖,对产品进行粗加工后再卖,对产品进行精加工后再卖.受加工能力和气温影响,粗加工一天只能加工200个,细加工一天只能加工100个,两种加工不能同时进行,且最多加工三天.
加工方式 | 加工成本 | 销售单位 | 售价 |
直接卖 | 0 | 个 | 2元/个 |
粗加工 | 1元/个 | 包装袋(一袋5个) | 30元/袋 |
精加工 | 2.5元/个 | 礼盒(一盒10个) | 85元/盒 |
假设所有粽子均能全部售出,则以下销售方式中利润最大的是____________.
方案一:不加工直接销售;
方案二:三天全部进行精加工,剩下的直接卖;
方案三:两天精加工,一天粗加工,剩下的直接卖;
方案四:两天粗加工,一天精加工,剩下的直接卖.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,是某企业甲、乙两位员工的能力测试结果的网状图,以O为圆心的五个同心圆分别代表能力水平的五个等级由低到高分别赋分1至5分,由原点出发的五条线段分别指向能力水平的五个维度,网状图能够更加直观的描述测试者的优势和不足,观察图形,有以下几个推断:
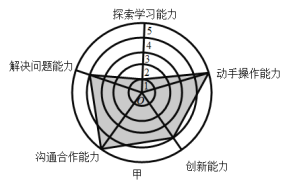
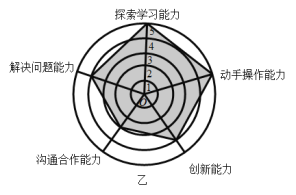
①甲和乙的动手操作能力都很强;
②缺少探索学习的能力是甲自身的不足;
③与甲相比乙需要加强与他人的沟通合作能力;
④乙的综合评分比甲要高.
其中合理的是( )
A.①③B.②④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com