
科目: 来源: 题型:
【题目】已知抛物线![]() 交
交![]() 轴于点(0,0)和点
轴于点(0,0)和点![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点(0,0)和点
轴于点(0,0)和点![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点(0,0)和点
轴于点(0,0)和点![]() …按此规律,抛物线
…按此规律,抛物线![]() 交
交![]() 轴于点(0,0)和点
轴于点(0,0)和点![]() (其中n为正整数),我们把抛物线
(其中n为正整数),我们把抛物线![]() 称为系数为
称为系数为![]() 的“关于原点位似”的抛物线族.
的“关于原点位似”的抛物线族.
(1)试求出![]() 的值;
的值;
(2)请用含n的代数式表示线段![]() 的长;
的长;
(3)探究下列问题:
①抛物线![]() 的顶点纵坐标
的顶点纵坐标![]() 与a、n有何数量关系?请说明理由;
与a、n有何数量关系?请说明理由;
②若系数为a的“关于原点位似”的抛物线族的各顶点坐标记为(T,S),请直接写出S和T所满足的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别与边AB,BC所在的直线相交,交点分别为E,F.
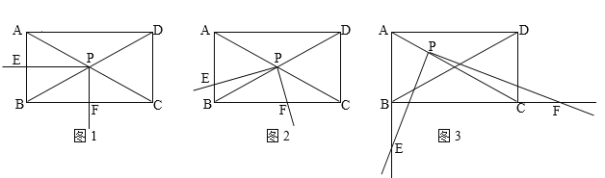
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)在(1)的基础上,现将三角板绕点P逆时针旋转![]() (0°<
(0°<![]() <60°)角,如图2,求
<60°)角,如图2,求![]() 的值;
的值;
(3)若与(2)相比只有如下变化,点P在线段AC上,且AP:PC=1:2,旋转角度![]() ,满足60°<
,满足60°<![]() <90°时,即如图3示,
<90°时,即如图3示,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.

(1)求一次函数、反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形,如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
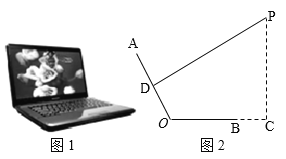
【题目】如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形.若显示屏AO与键盘BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,且PD⊥AO(此时点P为最佳视角),点C在OB的延长线上,PC⊥BC,BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)当∠AOC=115°时,线段PC的长比(1)中线段PC的长是增大还是减小?请通过计算说明.(结果精确到0.1cm,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.

(1)求证:直线AC是⊙O的切线;
(2)如果∠ACB=75°,⊙O的半径为2,求BD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1、图2两幅均不完整的统计图表.
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B |
| 0.25 |
C | 16 | b |
D | 8 |
|
合计 | a | 1 |
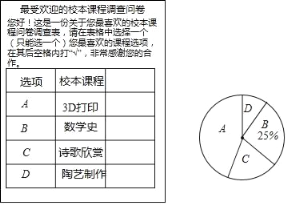
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】今年我国许多地方严重的“旱情”,为了鼓励居民节约用水,区政府计划实行两级收费制,即每月用水量不超过14吨(含14吨)时,每吨按政府补贴优惠价收费;每月超过14吨时,超过部分每吨按市场调节价收费.小英家1月份用水20吨,交水费29元;2月份用水18吨,交水费24元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】事业单位人员编制连进必考,现一事业单位需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方而进行量化考核.甲、乙、丙各项得分如下表:
笔试 | 面试 | 体能 | |
甲 | 84 | 80 | 88 |
乙 | 94 | 92 | 69 |
丙 | 81 | 84 | 78 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该单位规定:笔试、面试、体能分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com