
科目: 来源: 题型:
【题目】二次函数的图象过点(4,-5)和(0,3),且与x轴交于点M(-1,0)和N,
(1)求此二次函数的解析式;
(2)如果这二次函数的图像的顶点为点P,点O是坐标原点,求△OPN的面积.
(3)如果点R与点P关于x轴对称,判定以M、N、P、R为顶点的四边形的边之间的位置与度量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.

求证:
(1)△ABC≌△DCB;
(2)DE·DC=AE·BD.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE.

查看答案和解析>>
科目: 来源: 题型:
【题目】在标有平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形的六张形状、大小完全相等的纸片中,连续抽取其中两张纸片,被抽中的(所对应的图形)恰好是轴对称的概率是___________.
查看答案和解析>>
科目: 来源: 题型:
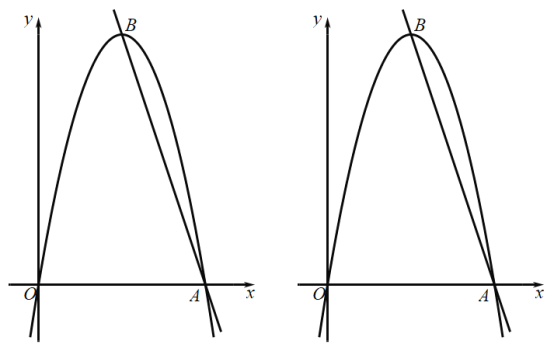
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的正半轴交于点A,抛物线的顶点为B,直线
轴的正半轴交于点A,抛物线的顶点为B,直线![]() 经过A,B两点,且
经过A,B两点,且![]() .
.
(1)求抛物线的解析式
(2)点P在第一象限内对称轴右侧的抛物线上,其横坐标为![]() ,连接OP,交对称轴于点C,过点C作
,连接OP,交对称轴于点C,过点C作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,连接
,连接![]() ,设线段
,设线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,交
,交![]() 于点F,点G是BE的中点,过点G作
于点F,点G是BE的中点,过点G作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,当
,当![]() 且
且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
查看答案和解析>>
科目: 来源: 题型:
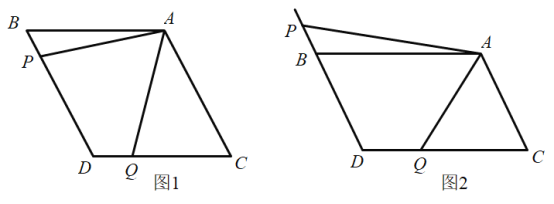
【题目】如图1,![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,且满足
上的点,且满足![]() .
.
(1)求证:![]()
(2)在图1中,是否存在与AP相等的线段?若存在,请找出来,并加以证明;若不存在,说明理由.
(3)若将“![]() 为
为![]() 上的点”改为:“
上的点”改为:“![]() 为DB延长线上的点”其他条件不变(如图2)若
为DB延长线上的点”其他条件不变(如图2)若![]() ,求线段
,求线段![]() 之间的数量关系(用含
之间的数量关系(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资,已知生产每件产品的成本是40元.在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利(年获利=年销售额一生产成本—投资)为z(万元).
(1)试写出y与x之间的函数关系式(不写x的取值范围);
(2)试写出z与x之间的函数关系式(不写x的取值范围);
(3)公司计划,在第一年按年获利最大确定销售单价进行销售;到第二年年底获利不低于1130万元,请借助函数的大致图象说明:第二年的销售单价x(元)应确定在什么范围内?
查看答案和解析>>
科目: 来源: 题型:
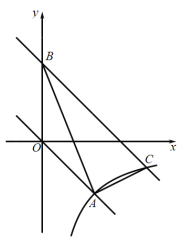
【题目】如图,在平面坐标系中,正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像都经过点
的图像都经过点![]() .
.
(1)分别求出这两个函数的解析式;
(2)将直线OA向上平移3个单位后与![]() 轴交于点B,与反比例函数的图像在第四象限内的交点为C,连接
轴交于点B,与反比例函数的图像在第四象限内的交点为C,连接![]() ,求
,求![]() 的面积
的面积
(3)在(2)的条件下,反比例![]() 函数的图像上是否存在点D使得
函数的图像上是否存在点D使得![]() ?若存在直接写出点D的坐标;若不存在,请说明理由.
?若存在直接写出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
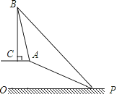
【题目】已知,如图,在笔山银子岩坡顶![]() 处的同一水平面上有一座移动信号发射塔
处的同一水平面上有一座移动信号发射塔![]() ,
,
笔山职中数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求:
.求:
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 移动信号发射塔
移动信号发射塔![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com