
科目: 来源: 题型:
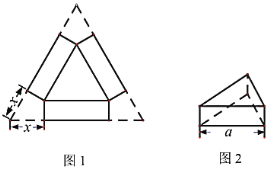
【题目】如图1,小明用一张边长为![]() 的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为
的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为![]() ,再折成如图2所示的无盖糖果盒,它的容积记为
,再折成如图2所示的无盖糖果盒,它的容积记为![]() .
.
(1)![]() 关于
关于![]() 的函数关系式是__________,自变量
的函数关系式是__________,自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)为探究![]() 随
随![]() 的变化规律,小明类比二次函数进行了如下探究:
的变化规律,小明类比二次函数进行了如下探究:
①列表:请你补充表格中的数据:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| 0 | 3.125 | ________ | 3.375 | ________ | 0.625 | 0 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:请你用光滑的曲线顺次连接各点.

(3)利用函数图象解决:
①该糖果盒的最大容积是__________;
②若该糖果盒的容积超过![]() ,请估计糖果盒的底边长
,请估计糖果盒的底边长![]() 的取值范围.(保留一位小数)
的取值范围.(保留一位小数)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1是三国时期的数学家赵爽创制的一幅“勾股圆方图”.将图2的矩形分割成四个全等三角形和一个正方形,恰好能拼成这样一个“勾股圆方图”,则该矩形与拼成的正方形的周长之比为________.
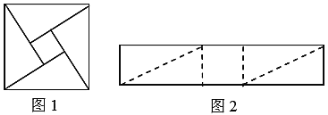
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,数轴上![]() 三个数所对应的点分别为
三个数所对应的点分别为![]() ,已知
,已知![]() ,且
,且![]() 的倒数是它本身,且
的倒数是它本身,且![]() 满足
满足![]() .
.
![]()
(1)求代数式![]() 的值:
的值:
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则与点
重合,则与点![]() 重合的点表示的数是_______;
重合的点表示的数是_______;
(3)请在数轴上确定一点![]() ,使得
,使得![]() ,则点
,则点![]() 表示的数是______.
表示的数是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某市有一块长为![]() 米,宽为
米,宽为![]() 米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为
米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为![]() 米的道路.(
米的道路.(![]() ).
).
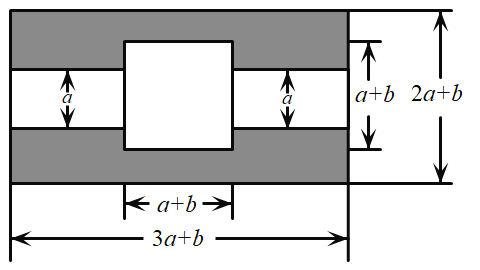
(1)①试用含![]() 的代数式表示绿化的面积是多少平方米?
的代数式表示绿化的面积是多少平方米?
②假设阴影部分可以拼成一个矩形.请你求出所拼矩形相邻两边的长:如果要使所拼矩形面积最大,求![]() 与
与![]() 满足的关系式;
满足的关系式;
(2)若![]() ,请求出绿化面积.
,请求出绿化面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】今年疫情期间,为防止疫惰扩散,人们见面的机会少了,但是随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.为此,李老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),进行调查.将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次参与调查的共有_______人:在扇形统计图中,表示“微信”的扇形圆心角的度数为_______;其它沟通方式所占的百分比为_______;
(2)将条形统计图补充完整;
(3)如果我国有13亿人在使用手机.①请估计最喜欢用“微信”进行沟通的人数:并:用科学计数法表示;②在全国使用手机的人中随机抽取一人,用频率估计概率,求抽取的恰好使用“QQ”的概率是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,BF交AC于G,连接CF.

(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,①试判断四边形ADCF的形状,并证明你的结论;
②若AB=8,BD=5,直接写出线段AG的长 .
查看答案和解析>>
科目: 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过![]() 时,材料温度降为600℃.如图,煅烧时温度
时,材料温度降为600℃.如图,煅烧时温度![]() 与时间
与时间![]() 成一次函敷关系:锻造时,温度
成一次函敷关系:锻造时,温度![]() 与时间
与时间![]() 成反比例函数关系。已知该材料初始温度是32℃.
成反比例函数关系。已知该材料初始温度是32℃.
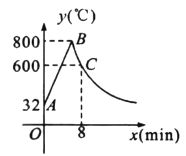
(1)分别求出材料煅烧和锻造时![]() 与
与![]() 的函数关系式,并且写出自变量
的函数关系式,并且写出自变量![]() 的取值范围;
的取值范围;
(2)根据工艺要求,当材料温度低于400℃时,须停止操作.那么锻造的操作时间最多有多长?.
(3)如果加工每个零件需要锻造12分钟,并且当材料温度低于400℃时,需要重新煅烧.通过计算说明加工第一个零件,一共需要多少分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com