
科目: 来源: 题型:
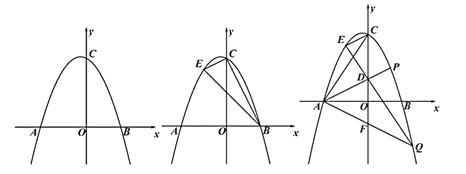
【题目】如图,已知抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴正半轴于
轴正半轴于![]() ,且
,且![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
(2)![]() 是第二象限抛物线上一点,坐标为
是第二象限抛物线上一点,坐标为![]() ,连接
,连接![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,![]() 是第一象限抛物线上一点,连接
是第一象限抛物线上一点,连接![]() 交
交![]() 轴于
轴于![]() ,连接
,连接![]() 并延长交抛物线与点
并延长交抛物线与点![]() ,连接
,连接![]() 交
交![]() 轴于
轴于![]() ,将点
,将点![]() 绕点
绕点![]() 逆时针旋转90°得到点
逆时针旋转90°得到点![]() 连接
连接![]() ,若
,若![]() 轴,求Q点坐标.
轴,求Q点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】六![]() 一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
![]() 求A、B两种品牌服装每套进价分别为多少元?
求A、B两种品牌服装每套进价分别为多少元?
![]() 该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC .
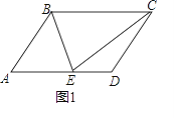
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
(1)求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数;
(2)将条形统计图补充完整;
(3)若规定:假期阅读3本及3本以上课外书者为完成假期作业,据此估计该校1500名学生中,完成假期作业的有多少名学生?

查看答案和解析>>
科目: 来源: 题型:
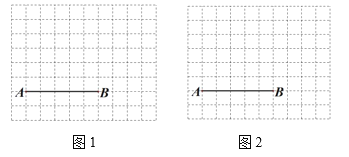
【题目】图1、图2分别是![]() 的网格,网格中每个小正方形的边长均为1,
的网格,网格中每个小正方形的边长均为1,![]() 、
、![]() 两点在小正方形的顶点上,请在图1、图2中各取一点
两点在小正方形的顶点上,请在图1、图2中各取一点![]() (点
(点![]() 必须在小正方形的顶点上),使以
必须在小正方形的顶点上),使以![]() 、
、![]() 、
、![]() 为顶点的三角形分别满足以下要求:
为顶点的三角形分别满足以下要求:
(1)在图1中画一个![]() ,使
,使![]() 是以
是以![]() 为斜边的直角三角形,且
为斜边的直角三角形,且![]() ;
;
(2)在图2中画一个![]() ,使
,使![]() 为等腰三角形,且
为等腰三角形,且![]() ,直接写出
,直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人都从![]() 出发经
出发经![]() 地去
地去![]() 地,乙比甲晚出发1分钟,两人同时到达
地,乙比甲晚出发1分钟,两人同时到达![]() 地,甲在
地,甲在![]() 地停留1分钟,乙在
地停留1分钟,乙在![]() 地停留2分钟,他们行走的路程
地停留2分钟,他们行走的路程![]() (米)与甲行走的时间
(米)与甲行走的时间![]() (分钟)之间的函数关系如图所示,则下列说法中正确的个数有( )
(分钟)之间的函数关系如图所示,则下列说法中正确的个数有( )
①甲到![]() 地前的速度为
地前的速度为![]()
②乙从![]() 地出发后的速度为
地出发后的速度为![]()
③![]() 、
、![]() 两地间的路程为
两地间的路程为![]()
④甲乙在行驶途中再次相遇时距离![]() 地
地![]()

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O,BD=6cm,AD=8cm,AB=10cm,点E从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点G从点C出发,沿CB方向匀速运动,速度为2cm/s;当一个点停止运动时,另一个点也停止运动.连接OE,过点G作GF∥BD,设运动时间为t(s)(0<t<4),解答下列问题:
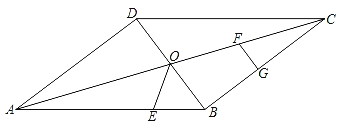
(1)当t为何值时,△BOE是等腰三角形?
(2)设五边形OEBGF面积为S,试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形OEBGF:S△ACD=19:40?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t,使得OB平分∠COE,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.
将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.
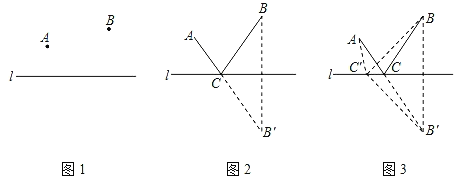
如图2,作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是所求的位置.
证明:如图3,在直线l上另取任一点C′,连结AC′,BC′,B′C′,
∵直线l是点B,B′的对称轴,点C,C′在l上,
∴CB=CB′,C′B=C′B′,
∴AC+CB=AC+ = .
在△AC′B′中,
∵AB′<AC′+C′B′
∴AC+CB<AC′+C′B′即AC+CB最小.
本问题实际上是利用轴对称变换的思想,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决(其中C在AB′与l的交点上,即A、C、B′三点共线).本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型.
1.简单应用
(1)如图4,在等边△ABC中,AB=6,AD⊥BC,E是AC的中点,M是AD上的一点,求EM+MC的最小值
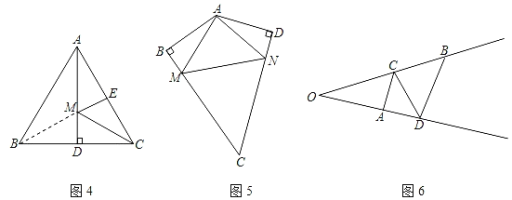
借助上面的模型,由等边三角形的轴对称性可知,B与C关于直线AD对称,连结BM,EM+MC的最小值就是线段 的长度,则EM+MC的最小值是 ;
(2)如图5,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M、N当△AMN周长最小时,∠AMN+∠ANM= °.
2.拓展应用
如图6,是一个港湾,港湾两岸有A、B两个码头,∠AOB=30°,OA=1千米,OB=2千米,现有一艘货船从码头A出发,根据计划,货船应先停靠OB岸C处装货,再停靠OA岸D处装货,最后到达码头B.怎样安排两岸的装货地点,使货船行驶的水路最短?请画出最短路线并求出最短路程.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来40天的销售单价p(元/kg)与时间 t(天)之间的函数表达式为p=![]() t+30;(1≤t≤40,t为整数),试销售当天(正式销售前一天)售出400kg,之后每天销售量比前一天减少5千克;
t+30;(1≤t≤40,t为整数),试销售当天(正式销售前一天)售出400kg,之后每天销售量比前一天减少5千克;
(1)试求每天销售利润W1(元)与时间t(天)之间的函数关系式;
(2)在销售前20天里,何时利润为4320元?
(3)为回馈新老顾客的支持,在实际销售中,超市决定每销售1kg水果就捐赠2元利润给“精准扶贫”对象.在日销售量不低于300kg的情况下,何时超市获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com