
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]()
![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,交
,交![]() 轴于点
轴于点![]() ,且抛物线的对称轴经过点
,且抛物线的对称轴经过点![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,点
,点![]() 是该抛物线上一点,连接
是该抛物线上一点,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直线![]() 及抛物线的函数表达式;
及抛物线的函数表达式;
(2)试问:![]() 轴上是否存在某一点
轴上是否存在某一点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() 为顶点的
为顶点的![]() 与
与![]() 相似?若相似,请求出此时点
相似?若相似,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() ,
,![]() 重合),过
重合),过![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,则
,则![]() 在直线
在直线![]() 上所截得的线段长度的最大值等于_______.(直接写出答案)
上所截得的线段长度的最大值等于_______.(直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
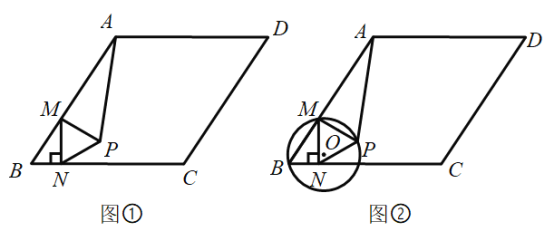
【题目】如图①,在菱形![]() 中
中![]() ,
,![]() ,边
,边![]() 上一动点
上一动点![]() 从点
从点![]() 出发向点
出发向点![]() 匀速运动,速度为
匀速运动,速度为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,以
,以![]() 为边长作等边
为边长作等边![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的异侧,连接
的异侧,连接![]() .点
.点![]() 的运动时间为
的运动时间为![]() .
.
(1)当![]() 时,
时,![]() _______
_______![]() ;(直接写出答案)
;(直接写出答案)
(2)连接![]() ,若
,若![]() 为等腰三角形,求
为等腰三角形,求![]() 的值;
的值;
(3)如图②,经过点![]() 、
、![]() 、
、![]() 作
作![]() ,连接
,连接![]() ,当
,当![]() 与
与![]() 相切时,则
相切时,则![]() 的值等于_______
的值等于_______![]() (直接写出答案)
(直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
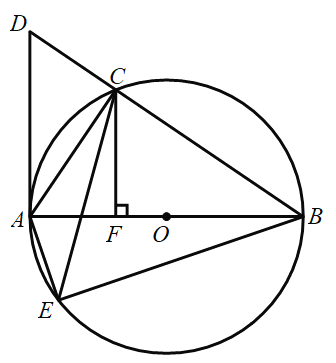
【题目】如图,![]() 内接于
内接于![]() ,
,![]() 是
是![]() 的直径,过点
的直径,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,
,![]() 是
是![]() 上一点,点
上一点,点![]() ,
,![]() 分别位于直径
分别位于直径![]() 异侧,连接
异侧,连接![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
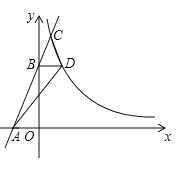
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]()
![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() 轴,交反比例函数
轴,交反比例函数![]()
![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的面积;
的面积;
(3)设![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴,交反比例函数
轴,交反比例函数![]()
![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形,求点
为顶点的四边形为平行四边形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了了解九年级学生上学期间平均每天的睡眠情况,现从全校![]() 名九年级学生中随机抽取了部分学生,调查了这些同学上学期间平均每天的睡眠时间
名九年级学生中随机抽取了部分学生,调查了这些同学上学期间平均每天的睡眠时间![]() (单位:小时),并根据调查结果列出统计表,绘制成扇形统计图,如图所示.请你根据图表提供的信息解答下列问题:
(单位:小时),并根据调查结果列出统计表,绘制成扇形统计图,如图所示.请你根据图表提供的信息解答下列问题:
平均每天睡眠时间分组统计表
组别序号 | 睡眠时间 | 人数(频数) |
|
|
|
|
|
|
|
|
|
|
|
|
平均每天睡眠时间扇形统计表
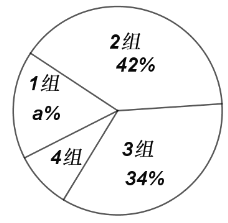
(1)![]() _______,
_______,![]() _______,
_______,![]() _______(
_______(![]() 为百分号前的数字);
为百分号前的数字);
(2)随机抽取的这部分学生平均每天睡眠时间的中位数落在_______组(填组别序号);
(3)估计全校![]() 名九年级学生中平均每天睡眠时间不低于
名九年级学生中平均每天睡眠时间不低于![]() 小时的学生有_______名;
小时的学生有_______名;
(4)若所抽查的睡眠时间![]() (小时)的
(小时)的![]() 名学生,其中
名学生,其中![]() 名男生和
名男生和![]() 名女生,现从这
名女生,现从这![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加个别访谈,请用列表或画树状图的方法求选取的
名学生参加个别访谈,请用列表或画树状图的方法求选取的![]() 名学生恰为
名学生恰为![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在某次防灾抗灾过程中,为了保障某市的抗灾物资供应,现有一批救灾物资由![]() ,
,![]() 两种型号的货车运输至该市.已知
两种型号的货车运输至该市.已知![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车共可满载救灾物资
型货车共可满载救灾物资![]() 吨,
吨,![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车共可满载救灾物资
型货车共可满载救灾物资![]() 吨.
吨.
(1)求![]() 辆
辆![]() 型货车和
型货车和![]() 辆
辆![]() 型货车分别能满载多少吨;
型货车分别能满载多少吨;
(2)已知这批救灾物资共![]() 吨,计划同时调用
吨,计划同时调用![]() ,
,![]() 两种型号的货车共
两种型号的货车共![]() 辆,并要求一次性将全部物资运送到该市,试求调用
辆,并要求一次性将全部物资运送到该市,试求调用![]() ,
,![]() 两种型号的货车的方案.
两种型号的货车的方案.
查看答案和解析>>
科目: 来源: 题型:
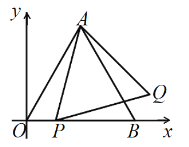
【题目】如图,平面直角坐标系![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 是
是![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,以
,以![]() 为边长,在
为边长,在![]() 的右侧作等边
的右侧作等边![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,则
,则![]() 与
与![]() 的函数关系式是________.
的函数关系式是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在正方形ABCD中,对角线AC、BD相交于点O,点E为线段BO上一点,连接CE,将CE绕点C顺时针旋转90°得到CF,连接EF交CD于点G.
(1)若AB=4,BE=![]() ,求△CEF的面积.
,求△CEF的面积.
(2)如图2,线段FE的延长线交AB于点H,过点F作FM⊥CD于点M,求证:BH+MG=![]() BE;
BE;
(3)如图3,点E为射线OD上一点,线段FE的延长线交直线CD于点G,交直线AB于点H,过点F作FM垂直直线CD于点M,请直接写出线段BH、MG、BE的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com