
科目: 来源: 题型:
【题目】问题提出:如何将一个长为17,宽为1的长方形经过剪一剪,拼一拼,形成一个正方形.(下列所有图中每个小方格的边长都为1,剪拼过程中材料均无剩余)
问题探究:我们从长为5,宽为1的长方形入手.

(1)如图①是一个长为5,宽为1的长方形.把这个长方形剪一剪、拼一拼后形成正方形,则正方形的面积应为_____________,设正方形的边长为![]() ,则
,则![]() _________;
_________;
(2)我们可以把有些带根号的无理数的被开方数表示成两个正整数平方和的形式,比如![]() .类比此,可以将(1)中的
.类比此,可以将(1)中的![]() 表示成
表示成![]() _____________;
_____________;
(3)![]() 的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为
的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为![]() ;类比此,(2)中的
;类比此,(2)中的![]() 可以理解为以长度________和__________为直角边的直角三角形斜边的长;
可以理解为以长度________和__________为直角边的直角三角形斜边的长;
(4)剪一剪:由(3)可画出如图②的分割线,把长方形分成![]() 五部分;
五部分;
(5)拼一拼:把图②中五部分拼接得到如图③的正方形;
问题解决:仿照上面的探究方法请把图④中长为17,宽为1的长方形剪一剪,在图⑤中画出拼成的正方形.(说明:图④的分割过程不作评分要求,只对图⑤中画出的最终结果评分)
![]()

查看答案和解析>>
科目: 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学在百货商场购进了A、B两种品牌的篮球,购买A品牌蓝球花费了2400元,购买B品牌蓝球花费了1950元,且购买A品牌蓝球数量是购买B品牌蓝球数量的2倍,已知购买一个B品牌蓝球比购买一个A品牌蓝球多花50元.
(1)求购买一个A品牌、一个B品牌的蓝球各需多少元?
(2)该学校决定再次购进A、B两种品牌蓝球共30个,恰逢百货商场对两种品牌蓝球的售价进行调整,A品牌蓝球售价比第一次购买时提高了10%,B品牌蓝球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌蓝球的总费用不超过3200元,那么该学校此次最多可购买多少个B品牌蓝球?
查看答案和解析>>
科目: 来源: 题型:
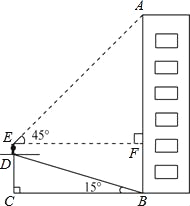
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=
,tan15°=![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】垃圾分类是对垃圾传统收集处理方式的改变,是对垃圾进行有效处理的一种科学管理方法.为了增强同学们垃圾分类的意识,某班举行了专题活动,对200件垃圾进行分类整理,得到下列统计图表,请根据统计图表回答问题:(其中A:可回收垃圾;B:厨余垃圾;C:有害垃圾;D:其它垃圾).
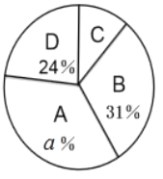
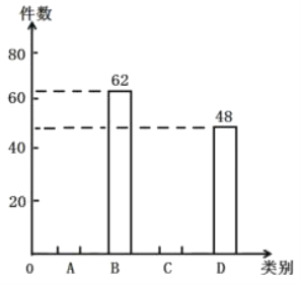
类别 | 件数 |
A | 70 |
B | b |
C | c |
D | 48 |
(1)![]() ________;
________;![]() ________;
________;
(2)补全图中的条形统计图;
(3)有害垃圾C在扇形统计图中所占的圆心角为多少?
查看答案和解析>>
科目: 来源: 题型:
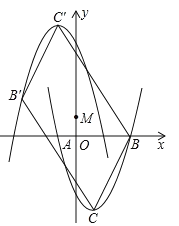
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴相交于A(﹣1,0),B(3,0)两点,点C为抛物线的顶点.点M(0,m)为y轴上的动点,将抛物线绕点M旋转180°,得到新的抛物线,其中B、C旋转后的对应点分别记为B'、C'.
(1)若a=1,求原抛物线的函数表达式;
(2)在(1)条件下,当四边形BCB'C'的面积为40时,求m的值;
(3)探究a满足什么条件时,存在点M,使得四边形BCB'C'为菱形?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
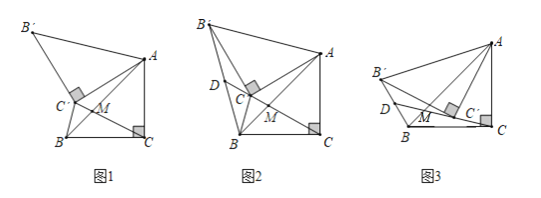
【题目】在△ABC中,∠ACB=90°,BC=AC=2,将△ABC绕点A顺时针方向旋转α角(0°<α<180°)至△AB'C'的位置.
问题探究:
(1)如图1,当旋转角为60°时,连接C'C与AB交于点M,则C'C= ,![]() .
.
(2)如图2,在(1)条件下,连接BB',延长CC'交BB'于点D,求CD的长.
问题解决:
(3)如图3,在旋转的过程中,连线CC'、BB',CC'所在直线交BB'于点D,那么CD的长有没有最大值?如果有,求出CD的最大值:如果没有,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
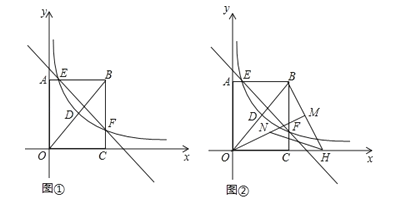
【题目】如图①,在矩形OABC中,OA=4,OC=3,分别以OC、OA所在的直线为x轴、y轴,建立如图所示的坐标系,连接OB,反比例函数y=![]() (x>0)的图象经过线段OB的中点D,并与矩形的两边交于点E和点F,直线l:y=kx+b经过点E和点F.
(x>0)的图象经过线段OB的中点D,并与矩形的两边交于点E和点F,直线l:y=kx+b经过点E和点F.
(1)写出中点D的坐标 ,并求出反比例函数的解析式;
(2)连接OE、OF,求△OEF的面积;
(3)如图②,将线段OB绕点O顺时针旋转一定角度,使得点B的对应点H恰好落在x轴的正半轴上,连接BH,作OM⊥BH,点N为线段OM上的一个动点,求HN+![]() ON的最小值.
ON的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com