
科目: 来源: 题型:
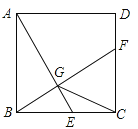
【题目】如图,已知正方形![]() 的边长为2,
的边长为2,![]() 是边
是边![]() 上的动点,
上的动点,![]() 交CD于F,垂足为G,连接
交CD于F,垂足为G,连接![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③点G运动的路径长为
;③点G运动的路径长为![]() ;④CG的最小值为
;④CG的最小值为![]() ;其中正确的是____________.
;其中正确的是____________.
查看答案和解析>>
科目: 来源: 题型:
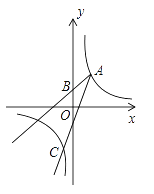
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为
都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为![]() ,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于
,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于![]() 之间部分的长度和为y,则y关于x的函数图象大致为( )
之间部分的长度和为y,则y关于x的函数图象大致为( )

A. 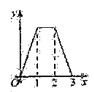 B.
B. 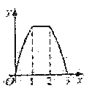 C.
C. 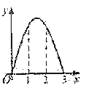 D.
D. 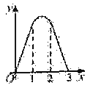
查看答案和解析>>
科目: 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
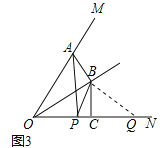
【题目】如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF、ON交于点B、点C,连接AB、PB.
(1)如图1,当P、Q两点都在射线ON上时,请直接写出线段AB与PB的数量关系;
(2)如图2,当P、Q两点都在射线ON的反向延长线上时,线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
(3)如图3,∠MON=60°,连接AP,设![]() =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
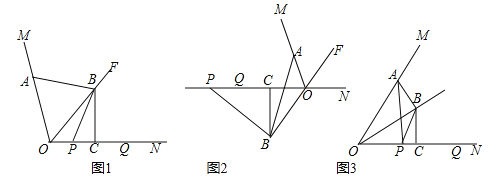
【答案】(1)AB=PB;(2)存在;(3)k=0.5.
【解析】试题分析:(1)结论:AB=PB.连接BQ,只要证明△AOB≌△PQB即可解决问题;
(2)存在.证明方法类似(1);
(3)连接BQ.只要证明△ABP∽△OBQ,即可推出![]() =
=![]() ,由∠AOB=30°,推出当BA⊥OM时,
,由∠AOB=30°,推出当BA⊥OM时, ![]() 的值最小,最小值为0.5,由此即可解决问题;
的值最小,最小值为0.5,由此即可解决问题;
试题解析:解:(1)连接:AB=PB.理由:如图1中,连接BQ.

∵BC垂直平分OQ,∴BO=BQ,∴∠BOQ=∠BQO,∵OF平分∠MON,∴∠AOB=∠BQO,∵OA=PQ,∴△AOB≌△PQB,∴AB=PB.
(2)存在,理由:如图2中,连接BQ.
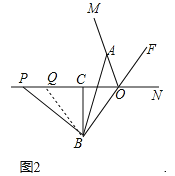
∵BC垂直平分OQ,∴BO=BQ,∴∠BOQ=∠BQO,∵OF平分∠MON,∠BOQ=∠FON,∴∠AOF=∠FON=∠BQC,∴∠BQP=∠AOB,∵OA=PQ,∴△AOB≌△PQB,∴AB=PB.
(3)连接BQ.
易证△ABO≌△PBQ,∴∠OAB=∠BPQ,AB=PB,∵∠OPB+∠BPQ=180°,∴∠OAB+∠OPB=180°,∠AOP+∠ABP=180°,∵∠MON=60°,∴∠ABP=120°,∵BA=BP,∴∠BAP=∠BPA=30°,∵BO=BQ,∴∠BOQ=∠BQO=30°,∴△ABP∽△OBQ,∴ ![]() =
=![]() ,∵∠AOB=30°,∴当BA⊥OM时,
,∵∠AOB=30°,∴当BA⊥OM时, ![]() 的值最小,最小值为0.5,∴k=0.5.
的值最小,最小值为0.5,∴k=0.5.
点睛:本题考查相似综合题、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.
【题型】解答题
【结束】
28
【题目】如图,已知抛物线y=ax2+![]() x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣
x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣![]() x﹣4与x轴交于点D,点P是抛物线y=ax2+
x﹣4与x轴交于点D,点P是抛物线y=ax2+![]() x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.

(1)试求该抛物线表达式;
(2)如图(1),若点P在第三象限,四边形PCOF是平行四边形,求P点的坐标;
(3)如图(2),过点P作PH⊥y轴,垂足为H,连接AC.
①求证:△ACD是直角三角形;
②试问当P点横坐标为何值时,使得以点P、C、H为顶点的三角形与△ACD相似?
查看答案和解析>>
科目: 来源: 题型:
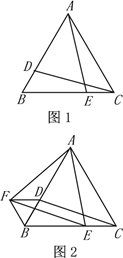
【题目】如图1,图2,△ABC是等边三角形,D、E分别是AB、BC边上的两个动点(与点A、B、C不重合),始终保持BD=CE.
(1)当点D、E运动到如图1所示的位置时,求证:CD=AE.
(2)把图1中的△ACE绕着A点顺时针旋转60°到△ABF的位置(如图2),分别连结DF、EF.
①找出图中所有的等边三角形(△ABC除外),并对其中一个给予证明;
②试判断四边形CDFE的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
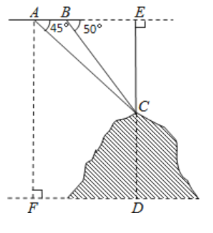
(1)直接写出∠ACB的大小;
(2)求这座山的高度CD.
查看答案和解析>>
科目: 来源: 题型:
【题目】据报载,在“百万家庭低碳行,垃圾分类要先行”活动中,某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查,并将调查结果分别绘成条形图(图1)、扇形图(图2).
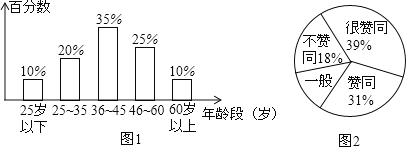
(1)图2中所缺少的百分数是_________;
(2)这次随机调查中,如果公民年龄的中位数是正整数,那么这个中位数所在年龄段是_________(填写年龄段);
(3)这次随机调查中,年龄段是“25岁以下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是________;
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有_______名.
查看答案和解析>>
科目: 来源: 题型:
【题目】列方程或方程组解应用题:
北京市实施交通管理新措施以来,全市公共交通客运量显著增加.据统计,2008年10月11日到2009年2月28日期间,地面公交日均客运量与轨道交通日均客运量总和为1696万人次,地面公交日均客运量比轨道交通日均客运量的4倍少69万人次.在此期间,地面公交和轨道交通日均客运量各为多少万人次?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以π cm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为______时,BP与⊙O相切.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com