
科目: 来源: 题型:
【题目】已知抛物线![]() ,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
(Ⅰ)求点A,B和点C的坐标;
(Ⅱ)已知P是线段![]() 上的一个动点.
上的一个动点.
①若![]() 轴,交抛物线于点Q,当
轴,交抛物线于点Q,当![]() 取最大值时,求点P的坐标;
取最大值时,求点P的坐标;
②求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() ,点
,点![]() ,点E,F分别在边
,点E,F分别在边![]() ,
,![]() 上.沿着
上.沿着![]() 折叠该纸片,使得点A落在
折叠该纸片,使得点A落在![]() 边上,对应点为
边上,对应点为![]() ,如图①.再沿
,如图①.再沿![]() 折叠,这时点E恰好与点C重合,如图②.
折叠,这时点E恰好与点C重合,如图②.

(Ⅰ)求点C的坐标;
(Ⅱ)将该矩形纸片展开,再折叠该矩形纸片,使点O与点F重合,折痕与![]() 相交于点P,展开矩形纸片,如图③.
相交于点P,展开矩形纸片,如图③.
①求![]() 的大小;
的大小;
②点M,N分别为![]() ,
,![]() 上的动点,当
上的动点,当![]() 取得最小值时,求点N的坐标(直接写出结果即可).
取得最小值时,求点N的坐标(直接写出结果即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】某剧院举行专场音乐会,成人票每张20元,学生票每张5元. 暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案一:购买一张成人票赠送一张学生票;方案二:按总价的90%付款. 某校有4名老师带队,与若干名(不少于4人)学生一起听音乐会.设学生人数为![]() 人,
人,![]() (
(![]() 为整数).
为整数).
(1)根据题意填表:
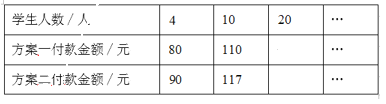
(2)设方案一付款总金额为![]() 元,方案二付款总金额为
元,方案二付款总金额为![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若用两种方案购买音乐会的花费相同,则听音乐会的学生有 人;
②若有60名学生听音乐会,则用方案 购买音乐会票的花费少;
③若用一种方案购买音乐会票共花费了![]() 元,则用方案 购买音乐会票,使听音乐的学生人数多.
元,则用方案 购买音乐会票,使听音乐的学生人数多.
查看答案和解析>>
科目: 来源: 题型:
【题目】在某中学开展的“好书伴我成长”读书活动中,为了解八年级320名学生读书情况,随机调查了八年级部分学生读书的册数. 根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
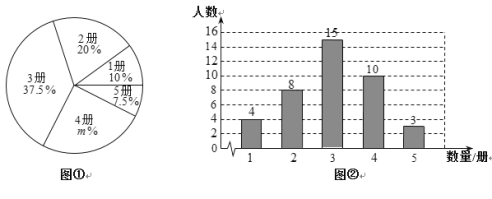
(1)本次接受调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)求统计的这组数据的平均数、众数和中位数;
(3)根据统计的样本数据,估计该校读书超过3册的学生人数.
查看答案和解析>>
科目: 来源: 题型:
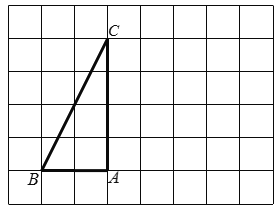
【题目】如图,在每个小正方形的边长为![]() 的网格中,△
的网格中,△![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上.
均在格点上.
(1)![]() 的长等于_____________;
的长等于_____________;
(2)在如图所示的网格中,将△![]() 绕点
绕点![]() 旋转,使得点
旋转,使得点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,得到△
上,得到△![]() ,请用无刻度的直尺,画出△
,请用无刻度的直尺,画出△![]() ,并简要说明这个三角形的各个顶点是如何找到的(不要求证明)__________.
,并简要说明这个三角形的各个顶点是如何找到的(不要求证明)__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的自变量x与函数值y的部分对应值如下表:
)的自变量x与函数值y的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … |
| 3 |
| 3 | … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②3是关于
;②3是关于![]() 的方程
的方程![]() 的一个根;③
的一个根;③![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2/span>D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出
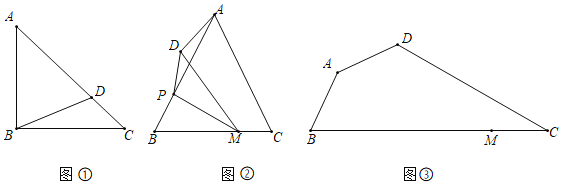
(1)如图①,在等腰Rt△ABC中,斜边AC=4,点D为AC上一点,连接BD,则BD的最小值为 ;
问题探究
(2)如图②,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,求AD的最小值;
问题解决
(3)如图③,四边形ABCD是规划中的休闲广场示意图,其中∠BAD=∠ADC=135°,∠DCB=30°,AD=2![]() km,AB=3km,点M是BC上一点,MC=4km.现计划在四边形ABCD内选取一点P,把△DCP建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路BP、MP,从实用和美观的角度,要求满足∠PMB=∠ABP,且景观绿化区面积足够大,即△DCP区域面积尽可能小.则在四边形ABCD内是否存在这样的点P?若存在,请求出△DCP面积的最小值;若不存在,请说明理由.
km,AB=3km,点M是BC上一点,MC=4km.现计划在四边形ABCD内选取一点P,把△DCP建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路BP、MP,从实用和美观的角度,要求满足∠PMB=∠ABP,且景观绿化区面积足够大,即△DCP区域面积尽可能小.则在四边形ABCD内是否存在这样的点P?若存在,请求出△DCP面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
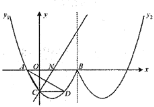
【题目】如图,曲线![]() 是抛物线的一部分,与
是抛物线的一部分,与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且表达式
,且表达式![]() ,曲线
,曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求![]() 三点的坐标和曲线
三点的坐标和曲线![]() 的表达式;
的表达式;
(2)过点![]() 作
作![]() 轴交曲线
轴交曲线![]() 于点
于点![]() ,连结
,连结![]() ,在曲线
,在曲线![]() .上有一点
.上有一点![]() ,使得四边形
,使得四边形![]() 为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点
为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com