
科目: 来源: 题型:
【题目】对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
科目: 来源: 题型:
【题目】在⊙O中,AB为直径,点C为圆上一点,将劣弧![]() 沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )

A.35°B.40°C.45°D.65°
查看答案和解析>>
科目: 来源: 题型:
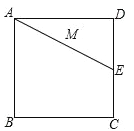
【题目】如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )
A.![]() cm或
cm或![]() cm B.
cm B.![]() cm C.
cm C.![]() cm或
cm或![]() cm D.
cm D.![]() cm或
cm或![]() cm
cm
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .直线
.直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
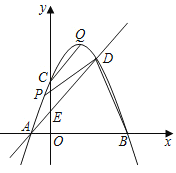
,点![]() 是抛物线的顶点,设直线
是抛物线的顶点,设直线![]() 上方的抛物线上的动点
上方的抛物线上的动点![]() 的横坐标为
的横坐标为![]() .
.
(1)连接![]() ,求证:四边形
,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)连接![]() ,
,![]() ,当
,当![]() 为何值时
为何值时![]() ?
?
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 为等腰直角三角形?若存在,请求出点
为等腰直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:有三条边相等的四边形称为三等边四边形.
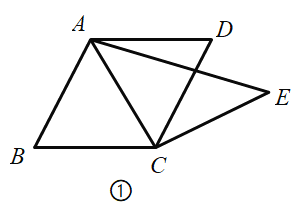
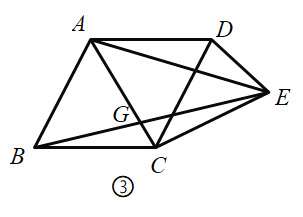
(1)如图①,平行四边形![]() 中,对角线
中,对角线![]() 平分
平分![]() ,将线段
,将线段![]() 绕点
绕点![]() 旋转一个角度
旋转一个角度![]() 至
至![]() ,连接
,连接![]() .
.
①求证:四边形![]() 是三等边四边形;
是三等边四边形;
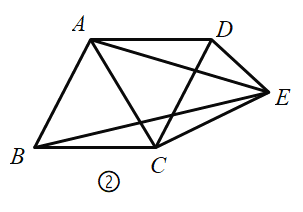
②如图②,连接![]() ,
,![]() .求证:
.求证:![]() ;
;
(2)如图,在(1)的条件下,设![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,求以
,求以![]() ,
,![]() 和
和![]() 为边的三角形的面积.
为边的三角形的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为直径,过点
为直径,过点![]() 的直线
的直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是弦
是弦![]() 延长线上一点,
延长线上一点,![]() ,
,![]() 的平分线与
的平分线与![]() 分别相交于点
分别相交于点![]() ,
,![]() ,
,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() ,与
,与![]() ,
,![]() 的延长线分别交于点
的延长线分别交于点![]() ,
,![]() .
.
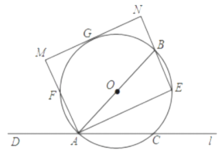
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
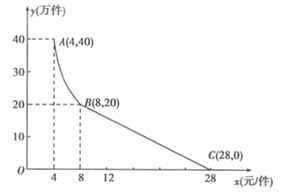
【题目】“净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上(![]() ),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了争创全国文明城市“六连冠”,写好2020年包头文明“答卷”,我市某班学生开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式对全年级同学进行卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个等级,划分等级后的数据整理如下表:

同时该班又抽取了班里的8名学生(分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ),进行垃圾分类投放检测,检测结果如下表)其中“√”表示投放正确,“×”表示投放错误.
),进行垃圾分类投放检测,检测结果如下表)其中“√”表示投放正确,“×”表示投放错误.

根据上表回答问题:
(1)求本次问卷调查取样的样本容量和表中![]() 的值;
的值;
(2)检测结果中,有几名学生正确投放了至少三类垃圾?请列举出这几名学生;
(3)为进一步了解学生垃圾分类的投放情况,从检测结果是“有害垃圾”投放错误的学生巾随机抽取2名进行访谈,请用列表或树状图法求抽到学生![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
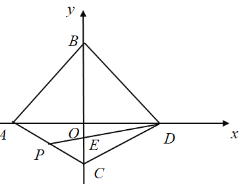
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 在
在![]() 轴负半轴上,且
轴负半轴上,且![]() ,把
,把![]() 沿
沿![]() 轴翻折,使点
轴翻折,使点![]() 落在
落在![]() 轴上的点
轴上的点![]() 处,点
处,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,则直线
,则直线![]() 的解析式为__________.
的解析式为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com