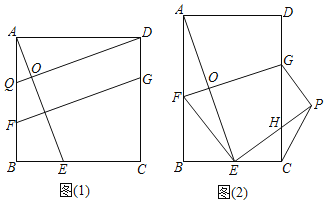
【题目】（1）证明推断：如图（1），在正方形中，点，分别在边，上，于点，点，分别在边，上，．

①求证：；

②推断：的值为　 　；

（2）类比探究：如图（2），在矩形中，（为常数）．将矩形沿折叠，使点落在边上的点处，得到四边形，交于点，连接交于点．试探究与CP之间的数量关系，并说明理由；

（3）拓展应用：在（2）的条件下，连接，当时，若，，求的长．

请你根据统计表中提供的信息回答下列问题：

（1）统计表中的 ， ；

（2）根据调查结果，请你估计该市2000名小学生中最喜欢“绘画”兴趣的人数；

（3）王姝和李要选择参加兴趣班，若他们每人从A、B、C、D四类兴趣班中随机选取一类，请用画树状图或列表格的方法，求两人恰好选中同一类的概率．

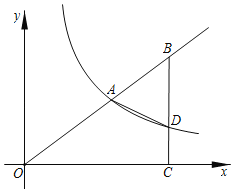
【题目】如图，在平面直角坐标系中，点在反比例函数的图象上，点在的延长线上，轴，垂足为，与反比例函数的图象相交于点，连接，．

（1）求该反比例函数的解析式；

（2）若，设点的坐标为，求线段的长．

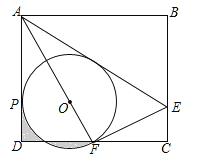
【题目】（2017四川省达州市，第16题，3分）如图，矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE翻折，使点B落在CD边F处，连接AF，在AF上取点O，以O为圆心，OF长为半径作⊙O与AD相切于点P．若AB=6，BC=，则下列结论：①F是CD的中点；②⊙O的半径是2；③AE=CE；④．其中正确结论的序号是__________．

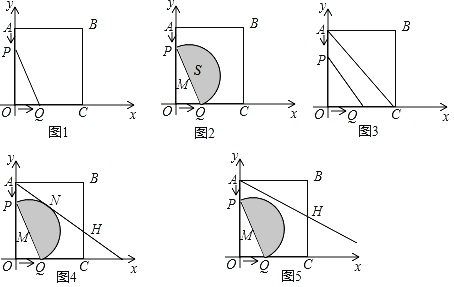
如图，在平面直角坐标系中，A(0，8)，C(6，0)，以O，A，C为顶点作矩形OABC，动点P从点A出发，沿AO以4个单位每秒的速度向O运动；同时动点Q从点O出发沿OC以3个单位每秒的速度向C运动．设运动时间为t，当动点P，Q中的任何一个点到达终点后，两点同时停止运动．连接PQ．

（情景导入）当t＝1时，求出直线PQ的解析式．

（深入探究）①连接AC，若△POQ与△AOC相似，求出t的值．

②如图，取PQ的中点M，以QM为半径向右侧作半圆M，直接写出半圆M的面积的最小值，并直接写出此时t的值．

（拓展延伸）如图，过点A作半圆M的切线，交直线BC于点H，于半圆M切于点N．

①在P，Q的整个运动过程中，点H的运动路径为　 　．

②若固定点H(6，2)不动，则在整个运动过程中，半圆M能否与梯形AOCH相切？若能，求出此时t的值；若不能，请证明．

（1）根据题意，完成下面问题：

①把下表补充完整（直接写在横线上）：

②从第1个月进行升级改造后，第　 　个月的产量开始超过未升级改造时的产量；

（2）若该基地第x个月（1≤x≤5，且x是整数）的产量为y万盒，求y关于x的函数关系式；

（3）已知每条生产线的升级改造费是30万元，每盒药品可获利3元．设从第1个月开始升级改造后，生产药品所获总利润为W1万元；同时期内，不升级改造所获总利润为W2万元设至少到第n个月（n为正整数）时，W1大于W2，求n的值．（利润＝获利﹣改造费）

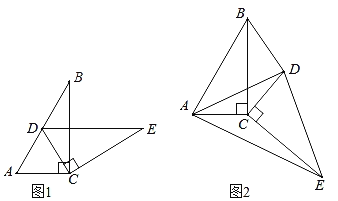
数学活动课上，老师让同学们以“三角形的旋转”为主题开展数学活动，△ABC和△DEC是两个全等的直角三角形纸片，其中∠ACB＝∠DCE＝90°，∠B＝∠E＝30°，AB＝DE＝4．

解决问题：

（1）如图1，智慧小组将△DEC绕点C顺时针旋转，发现当点D恰好落在AB边上时，DE∥AC，请你帮他们证明这个结论；

（2）缜密小组在智慧小组的基础上继续探究，当△DEC绕点C继续旋转到如图2所示的位置时，连接AE、AD、BD，他们提出S△BDC＝S△AEC，请你帮他们验证这一结论是否正确，并说明理由．

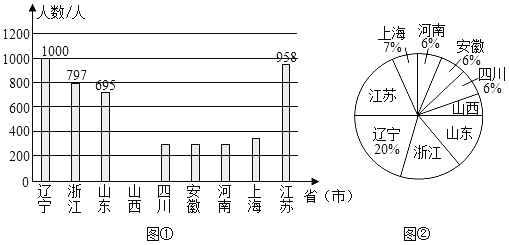
请解答下列问题：

（1）①上述省市2月9日当天驰援武汉的医护工作者的总人数为　 　人；

②请将图①的条形统计图补充完整；

（2）请求出图②的扇形统计图中“山西”所对应扇形的圆心角的度数；

（3）本次河北驰援武汉的医护工作者中，有5人报名去重症区，王医生和李医生就在其中，若从报名的5人中随机安排2人，求同时安排王医生和李医生的概率．

（分析问题）一时间，大家议论开了. 同学甲说：“可以利用代数方法，建立平面直角坐标系，利用函数的知识解决”，同学乙说：“也可以利用几何方法…”同学丙说：“我还有其他的几何证法”……

（解决问题）请你用两种方法解决问题

方法一（用代数方法）：

方法二（用几何方法）：

（1）8△9＝　 　；

（2）若x△3＝11，求x的值；

（3）求代数式﹣x△4的最小值．