
科目: 来源: 题型:
【题目】如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.
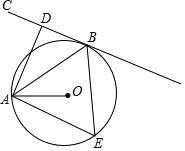
(1)求证:AB平分∠OAD;
(2)若点E是优弧 ![]() 上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)
上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)
查看答案和解析>>
科目: 来源: 题型:
【题目】中国是世界上13个贫水国家之一.某校有800名在校学生,学校为鼓励学生节约用水,展开“珍惜水资源,节约每一滴水”系列教育活动.为响应学校号召,数学小组做了如下调查:
小亮为了解一个拧不紧的水龙头的滴水情况,记录了滴水时间和烧杯中的水面高度,如图1.小明设计了调查问卷,在学校随机抽取一部分学生进行了问卷调查,并制作出统计图.如图2和图3.
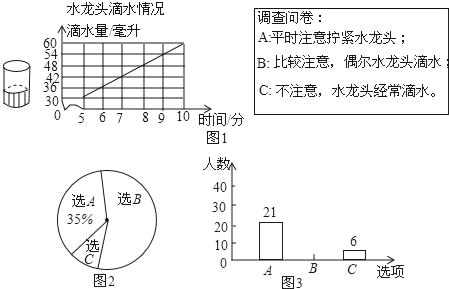
经结合图2和图3回答下列问题:
(1)参加问卷调查的学生人数为 人,其中选C的人数占调查人数的百分比为 .
(2)在这所学校中选“比较注意,偶尔水龙头滴水”的大概有 人.若在该校随机抽取一名学生,这名学生选B的概率为 .
请结合图1解答下列问题:
(3)在“水龙头滴水情况”图中,水龙头滴水量(毫升)与时间(分)可以用我们学过的哪种函数表示?请求出函数关系式.
(4)为了维持生命,每人每天需要约2400毫升水,该校选C的学生因没有拧紧水龙头,2小时浪费的水可维持多少人一天的生命需要?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
①AD是∠BAC的平分线;
②CD是△ADC的高;
③点D在AB的垂直平分线上;
④∠ADC=61°.
其中正确的有( ).
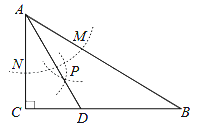
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
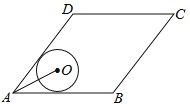
A.5 B.6 C.2![]() D.3
D.3![]()
查看答案和解析>>
科目: 来源: 题型:
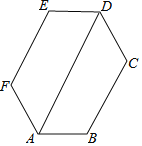
【题目】如图,六边形ABCDEF的内角都相等, ![]() ,则下列结论成立的个数是
,则下列结论成立的个数是![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() 四边形ACDF是平行四边形;
四边形ACDF是平行四边形; ![]() 六边形ABCDEF既是中心对称图形,又是轴对称图形.
六边形ABCDEF既是中心对称图形,又是轴对称图形.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目: 来源: 题型:
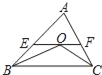
【题目】如图,在△ABC中,点O是∠ABC和∠ACB两个内角平分线的交点,过点O作EF∥BC分别交AB,AC于点E,F,已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
A. 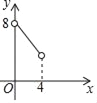 B.
B. 
C. 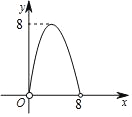 D.
D. 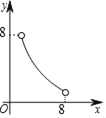
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣1,![]() ),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
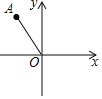
A.(0,﹣2)B.(1,﹣![]() )C.(2,0)D.(
)C.(2,0)D.(![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标;
(4)在平面内,是否存在点M使点A、B、C、M构成平行四边形,如果存在,直接写出M坐标;如果不存在,请说明理由.
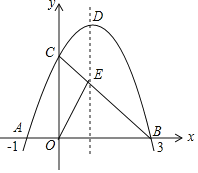
查看答案和解析>>
科目: 来源: 题型:
【题目】折纸是一种许多人熟悉的活动.近些年,经过许多人的努力,已经找到了多种将正方形折纸的一边三等分的精确折法,下面探讨其中的一种折法:
(综合与实践)
操作一:如图1,将正方形纸片ABCD对折,使点A与点D重合,点B与点C重合,再将正方形纸片ABCD展开,得到折痕MN;
操作二:如图2,将正方形纸片ABCD的右上角沿MC折叠,得到点D的对应的点为D′;
操作三:如图3,将正方形纸片ABCD的左上角沿MD′折叠再展开,折痕MD′与边AB交于点P;
(问题解决)
请在图3中解决下列问题:
(1)求证:BP=D′P;
(2)AP:BP= ;
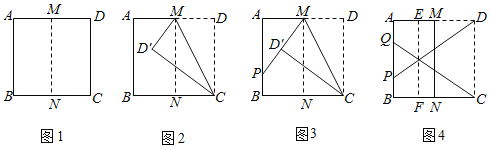
(拓展探究)
(3)在图3的基础上,将正方形纸片ABCD的左下角沿CD′折叠再展开,折痕CD′与边AB交于点Q.再将正方形纸片ABCD过点D′折叠,使点A落在AD边上,点B落在BC边上,然后再将正方形纸片ABCD展开,折痕EF与边AD交于点E,与边BC交于点F,如图4.试探究:点Q与点E分别是边AB,AD的几等分点?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】武警战士乘一冲锋舟从![]() 地逆流而上,前往
地逆流而上,前往![]() 地营救受困群众,途经
地营救受困群众,途经![]() 地时,由所携带的救生艇将
地时,由所携带的救生艇将![]() 地受困群众运回
地受困群众运回![]() 地,冲锋舟继续前进,到
地,冲锋舟继续前进,到![]() 地接到群众后立刻返回
地接到群众后立刻返回![]() 地,途中曾与救生艇相遇.冲锋舟和救生艇距
地,途中曾与救生艇相遇.冲锋舟和救生艇距![]() 地的距离
地的距离![]() (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间![]() (分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.

(1)请直接写出冲锋舟从![]() 地到
地到![]() 地所用的时间.
地所用的时间.
(2)求水流的速度.
(3)冲锋舟将![]() 地群众安全送到
地群众安全送到![]() 地后,又立即去接应救生艇.已知救生艇与
地后,又立即去接应救生艇.已知救生艇与![]() 地的距离
地的距离![]() (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间![]() (分)之间的函数关系式为
(分)之间的函数关系式为![]() ,假设群众上下船的时间不计,求冲锋舟在距离
,假设群众上下船的时间不计,求冲锋舟在距离![]() 地多远处与救生艇第二次相遇?
地多远处与救生艇第二次相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com