
科目: 来源: 题型:
【题目】为了传承中华优秀传统文化,培养学生自主、团结协作能力,某校推出了以下四个项目供学生选择:A.家乡导游:B.艺术畅游:C.体育世界:D.博物旅行.学校规定:每个学生都必须报名且只能选择其中一个项目,学校对某班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图,请结合统计图中的信息,解答下列问题:
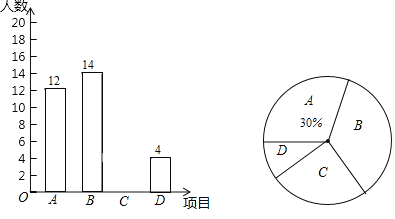
(1)求该班学生总人数;
(2)计算B项目所在扇形的圆心角的度数;
(3)将条形统计图补充完整;
(4)该校有1200名学生,请你估计选择“博物旅行”项目学生的人数.
查看答案和解析>>
科目: 来源: 题型:
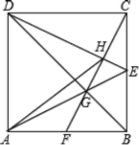
【题目】如图,正方形ABCD的边长为6,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①CF⊥DE;②![]() ;③AD=AH;④GH=
;③AD=AH;④GH=![]() ,其中正确结论的序号是__________.
,其中正确结论的序号是__________.
查看答案和解析>>
科目: 来源: 题型:
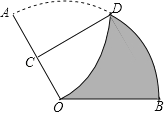
【题目】如图,一张扇形纸片OAB,∠AOB=120°,OA=6,将这张扇形纸片折叠,使点A与点O重合,折痕为CD,则图中未重叠部分(即阴影部分)的面积为( )
A.9![]() B.12π﹣9
B.12π﹣9![]() C.
C.![]() D.6π﹣
D.6π﹣![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果

下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,直线AB的解析式为y=﹣![]() x+4,抛物线y=﹣
x+4,抛物线y=﹣![]() +bx+c与y轴交于点A,与x轴交于点C(6,0),点P是抛物线上一动点,设点P的横坐标为m.
+bx+c与y轴交于点A,与x轴交于点C(6,0),点P是抛物线上一动点,设点P的横坐标为m.
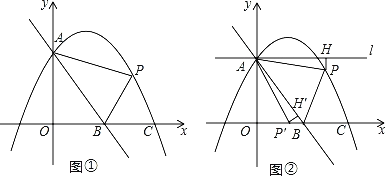
(1)求抛物线的解析式;
(2)当点P在第一象限内时,求△ABP面积的最大值,并求此时点P的坐标;
(3)如图②,当点P在y轴右侧时,过点A作直线l∥x轴,过点P作PH⊥l于点H,将△APH绕点A顺时针旋转,当点H的对应点H′恰好落在直线AB上时,点P的对应点P′恰好落在坐标轴上,请直接写出点P的横坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某数学活动小组在一次活动中,对一个数学问题做了如下研究:
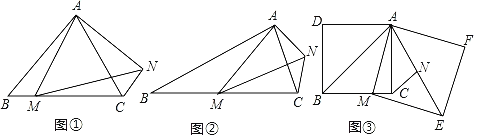
(问题发现)(1)如图①,在等边三角形ABC中,点M是BC边上任意一点,连接AM,以AM为边作等边三角形AMN,连接CN,则∠ABC和∠ACN的数量关系为 ;
(变式探究)(2)如图②,在等腰三角形ABC中,AB=BC,点M是BC边上任意一点(不含端点B,C,连接AM,以AM为边作等腰三角形AMN,使∠AMN=∠ABC,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(解决问题)(3)如图③,在正方形ADBC中,点M为BC边上一点,以AM为边作正方形AMEF,点N为正方形AMEF的中心,连接CN,AB,AE,若正方形ADBC的边长为8,CN=![]() ,直接写出正方形AMEF的边长.
,直接写出正方形AMEF的边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明根据学习函数的经验,对函数y=x+![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
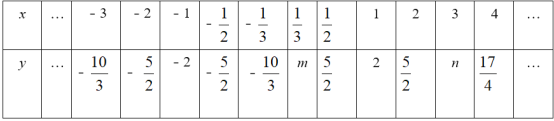
(2)下表列出了y与x的几组对应值,请写出m,n的值:m= ,n= ;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣![]() 时,x= .
时,x= .
②写出该函数的一条性质 .
③若方程x+![]() =t有两个不相等的实数根,则t的取值范围是 .
=t有两个不相等的实数根,则t的取值范围是 .
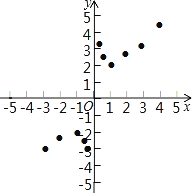
查看答案和解析>>
科目: 来源: 题型:
【题目】为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共需投入34万元.
(1)种植A,B两种蔬菜,每亩各需投入多少万元?
(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w关于m的函数关系式;
(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
查看答案和解析>>
科目: 来源: 题型:
【题目】襄阳卧龙大桥横跨汉江,是我市标志性建筑之一.某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121m,拉索AB与桥面AC的夹角为37°,从点A出发沿AC方向前进23.5m,在D处测得塔冠顶端E的仰角为45°.请你求出塔冠BE的高度(结果精确到0.1m.参考数据sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是半圆O的直径,AC是半圆内一条弦,点D是![]() 的中点,DB交AC于点G,过点A作半圆的切线与BD的延长线交于点M,连接AD.点E是AB上的一动点,DE与AC相交于点F.
的中点,DB交AC于点G,过点A作半圆的切线与BD的延长线交于点M,连接AD.点E是AB上的一动点,DE与AC相交于点F.
(1)求证:MD=GD;
(2)填空:①当∠DEA= 时,AF=FG;
②若∠ABD=30°,当∠DEA= 时,四边形DEBC是菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com