
科目: 来源: 题型:
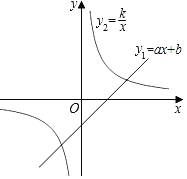
【题目】如图,已知一次函数y1=ax+b(a≠0)与反比例函数y2=![]() (k>0),两函数图象交于(4,1),(﹣2,n)两点.
(k>0),两函数图象交于(4,1),(﹣2,n)两点.
(1)求a,k的值;
(2)若y2>y1>0,求x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
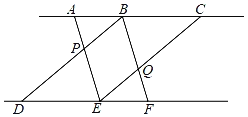
【题目】如图,已知AC∥DF,点B在AC上,点E在DF上,连结AE,BD相交于点P,连结CE,BF相交于点Q,若AB=EF,BC=DE.
(1)求证:四边形BPEQ为平行四边形;
(2)若DP=2BP,BF=3,CE=6.求证:四边形BPEQ为菱形.
查看答案和解析>>
科目: 来源: 题型:
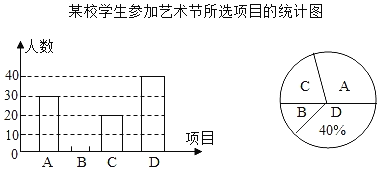
【题目】某校艺术节共开展了四项活动:器乐(A),舞蹈(B),绘画C),唱歌(D),每名学生只能参加一项活动.学校对学生所选的项目进行了抽样调查,并将调查结果绘制了如图两幅不完整的统计图,请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有 人;
(2)补全条形统计图.
(3)该校共有500名学生,请估计选择“绘画”的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:
①AD2+BC2=4;
②sin∠DAC=![]() ;
;
③若AC=BD,则DE=OE;
④若点P为BD的中点,则DE=2OE.
其中正确的是( )

A.①②③B.②③④C.③④D.②④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=a(x+1)(x﹣m)(a为非零常数,1<m<2),当x<﹣1时,y随x的增大而增大,说法正确的是( )
A.若图象经过点(0,1),则﹣![]() <a<0
<a<0
B.若x>﹣![]() 时,则y随x的增大而增大
时,则y随x的增大而增大
C.若(﹣2020,y1),(2020,y2)是函数图象上的两点,则y1<y2
D.若图象上两点(![]() ,y1),(
,y1),(![]() +n,y2)对一切正数n,总有y1>y2,则
+n,y2)对一切正数n,总有y1>y2,则![]() ≤m<2
≤m<2
查看答案和解析>>
科目: 来源: 题型:
【题目】为促进消费,杭州市政府开展发放政府补贴消费的“消费券”活动,一超市的月销售额逐步增加.据统计,2月份销售额为200万元,4月份销售额为500万元.若3,4月平均每月的增长率为x,则( )
A.200(1+x)=500B.200(1+x)+200+(1+x)2=500
C.200(1+x)2=500D.200+200(1+x)+200(1+x)2=500
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=x2﹣bx+c(b,c为常数,b>0)经过点A(﹣1,0),点M(m,0)是x轴正半轴上的动点.
(1)当b=2时,求抛物线的顶点坐标;
(2)点D(b,yD)在抛物线上,当AM=AD,m=3时,求b的值;
(3)点Q(b+![]() ,yQ)在抛物线上,当
,yQ)在抛物线上,当![]() AM+2
AM+2![]() QM的最小值为
QM的最小值为![]() 时,求b的值.(说明:yD表示D点的纵坐标,yQ表示Q点的纵坐标)
时,求b的值.(说明:yD表示D点的纵坐标,yQ表示Q点的纵坐标)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a>0)过点E(8,0),矩形ABCD的边AB在线段OE上(点A在点B的左侧),点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA:AD=1:3.
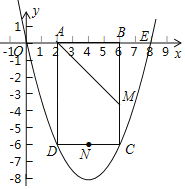
(1)求抛物线的解析式;
(2)F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值;
(3)在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为![]() ?若存在,求出点P的坐标;若不存在,请说明理由;
?若存在,求出点P的坐标;若不存在,请说明理由;
(4)矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL平分矩形的面积时,求抛物线平移的距离.
查看答案和解析>>
科目: 来源: 题型:
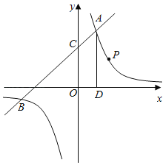
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)![]() ,
,![]() ;
;
(2)根据函数图象知,
①当![]() 时,
时,![]() 的取值范围是 ;
的取值范围是 ;
②当![]() 为 时,
为 时,![]() .
.
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 是反比例函数在第一象限的图象上一点,设直线
是反比例函数在第一象限的图象上一点,设直线![]() 与线段
与线段![]() 交于点
交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(4)点![]() 是
是![]() 轴上的一个动点,当△MBC为直角三角形时,直接写出点
轴上的一个动点,当△MBC为直角三角形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】一次函数y=kx+6与二次函数y=ax2+c的图象的一个交点坐标为(1,2),另一个交点是该二次函数图象的顶点.
(1)求k,a,c的值;
(2)过点A(0,m)(0<m<6)且垂直于y轴的直线与二次函数y=ax2+c的图象相交于B,C两点,点O为坐标原点,记W=OA2+BC2,求W关于m的函数解析式,并求W的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com