
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=kx+b与双曲线![]() 交于点A(1,n)和点B(-2,-1),点C是x轴的一个动点.
交于点A(1,n)和点B(-2,-1),点C是x轴的一个动点.
(1)①求m的值和点A的坐标;
②求直线l的表达式;
(2)若△ABC的面积等于6,直接写出点C的坐标.
查看答案和解析>>
科目: 来源: 题型:
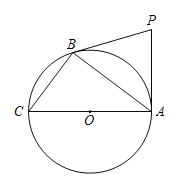
【题目】如图,PA,PB是⊙O的两条切线,A,B是切点,AC是⊙O的直径.
(1)若∠ACB=70°,求∠APB的度数;
(2)连接OP,若AB=8,BC=6,求OP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在边AD上,且DF=BE,连接DE,CF.
(1)求证:四边形AECF是矩形;
(2)若DE平分∠ADC,AB=5,AD=8,求tan∠ADE的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】在数学课上,老师提出如下问题:
已知:∠α,直线l和l上两点A,B.
求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.
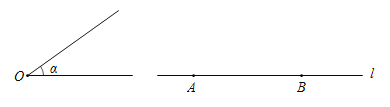
小刚的做法如下:
①以∠α的顶点O为圆心,任意长为半径作弧,交两边于M,N;以A为圆心,同样长为半径作弧,交直线l于点P;
②以P为圆心,MN的长为半径作弧,两弧交于点Q,作射线AQ;
③以B为圆心,任意长为半径作弧,交直线l于E,F;
④分别以E,F为圆心,大于![]() 长为半径作弧,两弧在直线l上方交于点G,作射线BG;
长为半径作弧,两弧在直线l上方交于点G,作射线BG;
⑤射线AQ与射线BG交于点C.Rt△ABC即为所求.
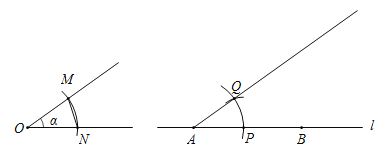
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
连接PQ
在△OMN和△AQP中,
∵ON=AP,PQ=NM,OM=AQ
∴△OMN ≌△AQP(__________)(填写推理依据)
∴∠PAQ=∠O=α
∵CE=CF,BE=BF
∴CB⊥EF(____________________________)(填写推理依据)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,是用图象反映储油罐内的油量V与输油管开启时间t的函数关系.观察这个图象,以下结论正确的有________________.
①随着输油管开启时间的增加,储油罐内的油量在减少;
②输油管开启10分钟时,储油罐内的油量是80立方米;
③如果储油罐内至少存油40立方米,那么输油管最多可以开启36分钟;
④输油管开启30分钟后,储油罐内的油量只有原油量的一半.
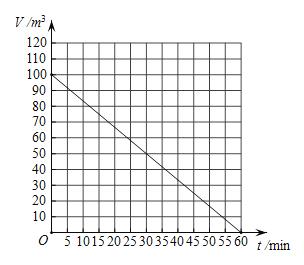
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相同,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各种多少两?设黄金重![]() 两,每枚白银重
两,每枚白银重![]() 两,根据题意可列方程组为____.
两,根据题意可列方程组为____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,边长为2的等边△ABC是三棱镜的一个横截面.一束光线ME沿着与AB边垂直的方向射入到BC边上的点D处(点D与B,C不重合),反射光线沿DF的方向射出去,DK与BC垂直,且入射光线和反射光线使∠MDK=∠FDK.设BE的长为x,△DFC的面积为y,则下列图象中能大致表示y与x的函数关系的是( )
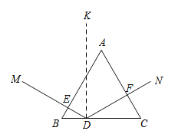
A. B.
B.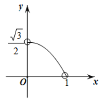 C.
C.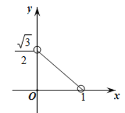 D.
D.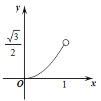
查看答案和解析>>
科目: 来源: 题型:
【题目】今年的新冠肺炎病毒侵袭武汉时,全中国第一时间组织对武汉的救援.这其中,我国自主研制的大型运输机“运20”,为在疫情初期向武汉快速转运大量物资和人员作出了重要贡献.“运20”起飞重量220吨,从立项到成功编入部队,经历了20多年,仅研究初期的预研经费就超过3 000 000 000元人民币.将3 000 000 000用科学记数法表示为( )
A.3×108B.0.3×1010C.3×109D.30×108
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A,B两点(点A在点B的左侧),直线
轴交于A,B两点(点A在点B的左侧),直线![]() 与抛物线交于
与抛物线交于![]() 两点,其中点
两点,其中点![]() 的横坐标为2.
的横坐标为2.
(1)求A,B两点的坐标及直线AC的表达式;
(2)P是线段AC上一动点(P与A,C不重合),过点P作![]() 轴的平行线交抛物线于点E,求
轴的平行线交抛物线于点E,求![]() 面积的最大值;
面积的最大值;
(3)点H是抛物线上一动点,在![]() 轴上是否存在点F,使得
轴上是否存在点F,使得![]() 四个点为顶点的四边形是平行四边形?如果存在请直接写出所有满足条件的点F坐标;如果不存在,请说明理由.
四个点为顶点的四边形是平行四边形?如果存在请直接写出所有满足条件的点F坐标;如果不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.

(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;
(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;
(3)在(2)的条件下,四边形PCFE的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com