
科目: 来源: 题型:
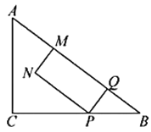
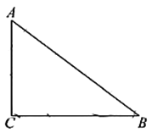
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒5个单位长度的速度沿
出发,以每秒5个单位长度的速度沿![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以相同的速度沿
出发,以相同的速度沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,当点
,当点![]() 运动到终点时,整个运动停止,设矩形
运动到终点时,整个运动停止,设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)①![]() 的长为 ;
的长为 ;
②用含![]() 的代数式表示线段
的代数式表示线段![]() 的长为 ;
的长为 ;
(2)当![]() 的长度为10时,求
的长度为10时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)当过点![]() 和点
和点![]() 的直线垂直于
的直线垂直于![]() 的一边时,直接写出
的一边时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
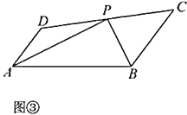
【题目】问题呈现:下图是小明复习全等三角形时遇到的一个问题并引发的思考,请帮助小明完成以下学习任务.

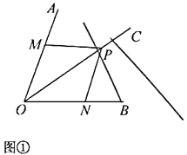
请根据小明的思路,结合图①,写出完整的证明过程.结论应用:
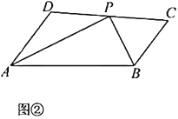
(1)如图②,在四边形![]() 中,
中,![]() ,
,![]() 的平分线和
的平分线和![]() 的平分线交于
的平分线交于![]() 边上点
边上点![]() .求证:
.求证:![]() ;
;
(2)在(1)的条件下,如图③,若![]() ,
,![]() .当
.当![]() 有一个内角是
有一个内角是![]() 时,
时,![]() 的面积是 .
的面积是 .
查看答案和解析>>
科目: 来源: 题型:
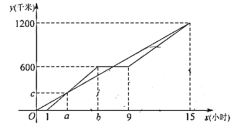
【题目】甲、乙两车沿同一条道路从![]() 地出发向1200
地出发向1200![]() 外的
外的![]() 地输送紧急物资,甲在途中休息了3小时,休息前后的速度不同,最后两车同时到达
地输送紧急物资,甲在途中休息了3小时,休息前后的速度不同,最后两车同时到达![]() 地,如图甲、乙两车到
地,如图甲、乙两车到![]() 地的距离
地的距离![]() (千米)与乙车行驶时间
(千米)与乙车行驶时间![]() (小时)之间的函数图象.
(小时)之间的函数图象.
(1)甲车休息前的行驶速度为 千米/时,乙车的速度为 千米/时;
(2)当9≤![]() ≤15,求甲车的行驶路程
≤15,求甲车的行驶路程![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)直接写出甲出发多长时间与乙在途中相遇.
查看答案和解析>>
科目: 来源: 题型:
【题目】某年级共有150名女生,为了解该校女生实心球成绩(单位:米)和仰卧起坐(单位:个)的情况,从中随机抽取30名女生进行测试,获得了她们的相关成绩,并对数据进行整理、描述和分析,下面给出了部分信息.
![]() .实心球成绩的频数分布表如下:
.实心球成绩的频数分布表如下:
分组 | 6.2≤ | 6.6≤ | 7.0≤ | 7.4≤ | 7.8≤ | 8.2≤ |
频数 | 2 |
| 10 | 6 | 2 | 1 |
![]() .实心球成绩在7.0≤
.实心球成绩在7.0≤![]() <7.4.这组的是:
<7.4.这组的是:
7.0 | 7.0 | 7.0 | 7.1 7.1 | 7.1 | 7.2 | 7.2 | 7.3 | 7.3 |
![]() .一分钟仰卧起坐成绩如图所示:
.一分钟仰卧起坐成绩如图所示:

根据以上信息,回答下列问题:
(1)①表中m的值为 ;
②抽取学生一分钟仰卧起坐成绩的中位数为 个;
(2)若实心球成绩达到7.2米及以上,成绩记为优秀,请估计全年级女生成绩达到优秀的人数.
(3)该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有2名女生的一分钟仰卧起坐成绩未抄录完整,当老师说这8名女生恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.
查看答案和解析>>
科目: 来源: 题型:
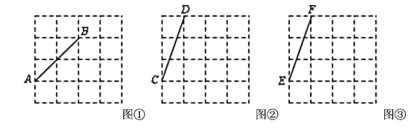
【题目】图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上,在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求长写出画法.
均在格点上,在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求长写出画法.
(1)在图①中以线段![]() 为边画一个直角△
为边画一个直角△![]() ;
;
(2)在图②中以线段![]() 为边画一个轴对称△
为边画一个轴对称△![]() ,使其面积为5;
,使其面积为5;
(3)在图③中以线段![]() 为边画一个轴对称四边形
为边画一个轴对称四边形![]() ,使其面积为6.
,使其面积为6.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,抛物线![]() 交
交![]() 正半轴于点
正半轴于点![]() ,将抛物线
,将抛物线![]() 先向右平移
先向右平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
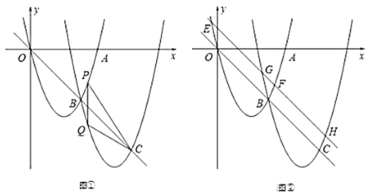
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物线
是抛物线![]() 上
上![]() (含端点)间的一点,作
(含端点)间的一点,作![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连按
,连按![]() ,
,![]() .当
.当![]() 的面积为
的面积为![]() 时, 求点
时, 求点![]() 的坐标;
的坐标;
(3)如图②,将直线![]() 向上平移,交抛物线
向上平移,交抛物线![]() 于点
于点![]() 、
、![]() ,交抛物线
,交抛物线![]() 于点
于点![]() 、
、![]() ,试判断
,试判断![]() 的值是否为定值,并说明理由.
的值是否为定值,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(方法回顾)
课本研究三角形中位线性质的方法
已知:如图①, 已知![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 两边中点.
两边中点.
求证:![]() ,
,![]()
证明:延长![]() 至点
至点![]() ,使
,使![]() , 连按
, 连按![]() .可证:
.可证:![]() ( )
( )
由此得到四边形![]() 为平行四边形, 进而得到求证结论
为平行四边形, 进而得到求证结论
(1)请根据以上证明过程,解答下列两个问题:
①在图①中作出证明中所描述的辅助线(请用![]() 铅笔作辅助线);
铅笔作辅助线);
②在证明的括号中填写理由(请在![]() ,
,![]() ,
,![]() ,
,![]() 中选择) .
中选择) .
(问题拓展)
(2)如图②,在等边![]() 中, 点
中, 点![]() 是射线
是射线![]() 上一动点(点
上一动点(点![]() 在点
在点![]() 的右侧),把线段
的右侧),把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,点
,点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() 、
、![]() .
.
①请你判断线段![]() 与
与![]() 的数量关系,并给出证明;
的数量关系,并给出证明;
②若![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
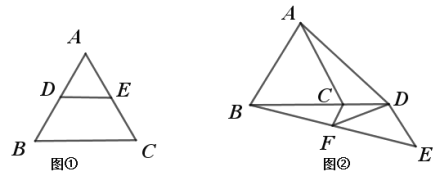
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com