
科目: 来源: 题型:
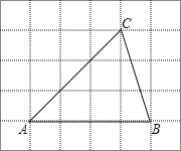
【题目】如图,将![]() 放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
![]() Ⅰ
Ⅰ![]() 的面积等于______;
的面积等于______;
![]() Ⅱ
Ⅱ![]() 若四边形DEFG是
若四边形DEFG是![]() 中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法
中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法![]() 不要求证明
不要求证明![]() ________________.
________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了如下的统计图1和图2,请根据图中相关信息,解决下列问题:
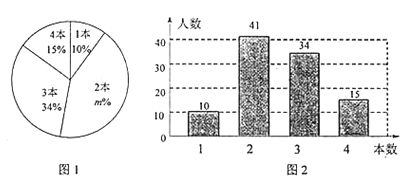
(Ⅰ)图1中![]() 的值为____________,共有____________名同学参与问卷调查;
的值为____________,共有____________名同学参与问卷调查;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ)全校共有学生1500人,根据样本数据,估计该校学生一个月阅读2本课外书的人数约为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知AB是⊙O的直径,C为⊙O上一点,OC=4,∠OAC=60°.
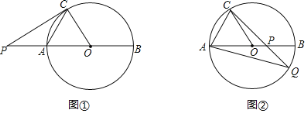
(Ⅰ)如图①,过点C作⊙O的切线,与BA的延长线交于点P,求∠P的大小;
(Ⅱ)如图②,P为AB上一点,CP延长线与⊙O交于点Q.若AQ=CQ,求∠APC的大小及PA的长.
查看答案和解析>>
科目: 来源: 题型:
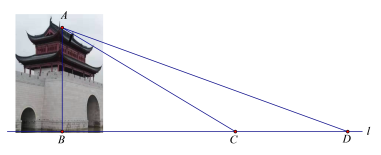
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中不超过200元的不打折,超过200元后的价格部分打7折.
设商品原价为x元,顾客购物金额为y元.
(I).根据题意,填写下表:
商品原价 | 100 | 150 | 250 | … |
甲商场购物金额(元) | 80 | … | ||
乙商场购物金额(元) | 100 | … |
(Ⅱ).分别就两家商场的让利方式写出y关于x的函数关系式;
(Ⅲ).若x≥500时,选择哪家商场去购物更省钱?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
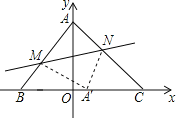
【题目】把△ABC放置在平面直角坐标系中,点A的坐标为(0,8),点B的坐标为(-6,0),点C的坐标为(8,0),M,N分别是线段AB,AC上的点,将△AMN沿直线MN翻折后,点A落在x轴上的A′处.
![]() Ⅰ
Ⅰ![]() 当MN∥x轴时,判断△A'CN的形状.
当MN∥x轴时,判断△A'CN的形状.
![]() Ⅱ
Ⅱ![]() 如图,当A'M⊥AB时.
如图,当A'M⊥AB时.
①求A'的坐标;②求MN的长.
![]() Ⅲ
Ⅲ![]() 当△A'MB是等腰三角形时,直接写出A'的坐标.
当△A'MB是等腰三角形时,直接写出A'的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() .过点
.过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .
.
(Ⅰ)求该抛物线的解析式及对称轴;
(Ⅱ)点![]() 在
在![]() 轴上,当
轴上,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标;
的坐标;
(Ⅲ)抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
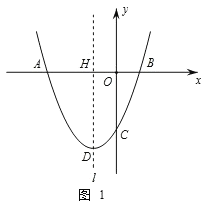
【题目】如图1,已知抛物线![]() 经过A(-3,0),B(1,0),C(0,-3)三点,其顶点为D,对称轴是直线
经过A(-3,0),B(1,0),C(0,-3)三点,其顶点为D,对称轴是直线![]() ,
,![]() 与x轴交于点H.
与x轴交于点H.
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴![]() 上的一个动点,求△PBC周长的最小值;
上的一个动点,求△PBC周长的最小值;
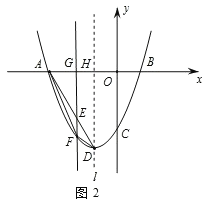
(3)如图2,若E是线段AD上的一个动点(E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①试求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com