
科目: 来源: 题型:
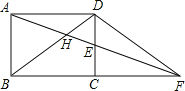
【题目】如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10![]() ,且tan∠EFC=
,且tan∠EFC=![]() ,那么AH的长为( )
,那么AH的长为( )
A. ![]() B.
B. ![]() C. 10D. 5
C. 10D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
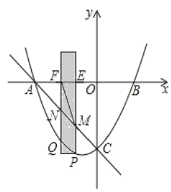
的坐标为![]() .有一宽度为1,长度足够长的矩形(阴影部分)沿
.有一宽度为1,长度足够长的矩形(阴影部分)沿![]() 轴方向平移,与
轴方向平移,与![]() 轴平行的一组对边交抛物线于点
轴平行的一组对边交抛物线于点![]() 和点
和点![]() ,交直线
,交直线![]() 于点
于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() 和点
和点![]() .
.
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)当点![]() 和
和![]() 都在线段
都在线段![]() 上时,连接
上时,连接![]() ,如果
,如果![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在矩形的平移过程中,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,若存在,求出点
为顶点的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
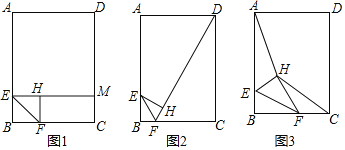
【题目】如图,点E,F分别在矩形ABCD的边AB,BC上,连接EF,将△BEF沿直线EF翻折得到△HEF,AB=8,BC=6,AE:EB=3:1.
(1)如图1,当∠BEF=45°时,EH的延长线交DC于点M,求HM的长;
(2)如图2,当FH的延长线经过点D时,求tan∠FEH的值;
(3)如图3,连接AH,HC,当点F在线段BC上运动时,试探究四边形AHCD的面积是否存在最小值?若存在,求出四边形AHCD的面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
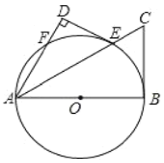
【题目】如图,已知![]() 是圆
是圆![]() 的直径,
的直径,![]() 是圆
是圆![]() 上一点,
上一点,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的切线
的切线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,
,
①求![]() 的值;②若点
的值;②若点![]() 为
为![]() 上一点,求
上一点,求![]() 最小值.
最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某文具店经销甲、乙两种不同的笔记本.已知:两种笔记本的进价之和为10元,甲种笔记本每本获利2元,乙种笔记本每本获利1元,马阳光同学买4本甲种笔记本和3本乙种笔记本共用了47元.
(1)甲、乙两种笔记本的进价分别是多少元?
(2)该文具店购入这两种笔记本共60本,花费不超过296元,则购买甲种笔记本多少本时该文具店获利最大?
(3)店主经统计发现平均每天可售出甲种笔记本350本和乙种笔记本150本.如果甲种笔记本的售价每提高1元,则每天将少售出50本甲种笔记本;如果乙种笔记本的售价每提高1元,则每天少售出40本乙种笔记本,为使每天获取的利润更多,店主决定把两种笔记本的价格都提高![]() 元,在不考虑其他因素的条件下,当
元,在不考虑其他因素的条件下,当![]() 定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字![]() 、
、![]() 、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,将球上的数字记为![]() ,求关于
,求关于![]() 的一元二次方程
的一元二次方程![]() 有实数根的概率;
有实数根的概率;
(2)从中任取一球,将球上的数字作为点的横坐标,记为![]() (不放回);再任取一球,将球上的数字作为点的纵坐标,记为
(不放回);再任取一球,将球上的数字作为点的纵坐标,记为![]() ,试用画树状图(或列表法)表示出点
,试用画树状图(或列表法)表示出点![]() 所有可能出现的结果,并求点
所有可能出现的结果,并求点![]() 落在第二象限内的概率.
落在第二象限内的概率.
查看答案和解析>>
科目: 来源: 题型:
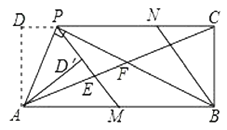
【题目】在矩形![]() 中,
中,![]() 为
为![]() 边上一点
边上一点![]() ,
,![]() .将
.将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .连接
.连接![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .现有以下结论:①连接
.现有以下结论:①连接![]() ,则
,则![]() 垂直平分
垂直平分![]() ;②四边形
;②四边形![]() 是菱形;③
是菱形;③![]() ;④若
;④若![]() ,则
,则![]() .其中正确的结论是________(填写所有正确结论的序号).
.其中正确的结论是________(填写所有正确结论的序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A. 用适当的统计图表示某班同学戴眼镜和不戴眼镜所占的比例,应绘制折线统计图
B. 为了解我市某区中小学生每月零花钱的情况,随机抽取其中800名学生进行调查,这次调查的样本是800名学生
C. “任意画出一个平行四边形,它是中心对称图形”是必然事件
D. 若点![]() 在第二象限,则点
在第二象限,则点![]() 在第一象限
在第一象限
查看答案和解析>>
科目: 来源: 题型:
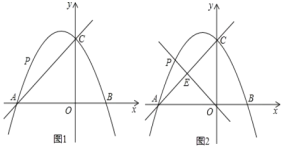
【题目】在平面直角坐标系中,抛物线y=-![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
(1)求抛物线的表达式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE∶OE=3∶8,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
![]() 概念理解:
概念理解:
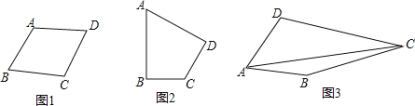
如图![]() ,在四边形
,在四边形![]() 中,添加一个条件使得四边形
中,添加一个条件使得四边形![]() 是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是________.
是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是________.
![]() 问题探究:
问题探究:
如图![]() ,在“等邻边四边形”
,在“等邻边四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,求对角线
,求对角线![]() 的长.
的长.
![]() 拓展应用:
拓展应用:
如图![]() ,“等邻边四边形”
,“等邻边四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为对角线,试探究
为对角线,试探究![]() ,
,![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com