
科目: 来源: 题型:
【题目】小明和小丽暑期参加工厂社会实践活动,师傅将他们工作第一周每天生产的合格产品的个数整理成如表两组数据,那么关于他们工作第一周每天生产的合格产品个数,下列说法中正确的是( )
小明 | 2 | 6 | 7 | 7 | 8 |
小丽 | 2 | 3 | 4 | 8 | 8 |
A. 小明的平均数小于小丽的平均数
B. 两人的中位数相同
C. 两人的众数相同
D. 小明的方差小于小丽的方差
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,点E是
,点E是![]() 边上的动点,将矩形
边上的动点,将矩形![]() 沿
沿![]() 折叠,点A落在点
折叠,点A落在点![]() 处,连接
处,连接![]() .
.
(1)如图,求证:![]() ;
;
(2)如图,若点![]() 恰好落在
恰好落在![]() 上,求
上,求![]() 的值;
的值;
(3)点E在![]() 边上运动的过程中,
边上运动的过程中,![]() 的度数是否存在最大值,若存在,求出此时线段
的度数是否存在最大值,若存在,求出此时线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
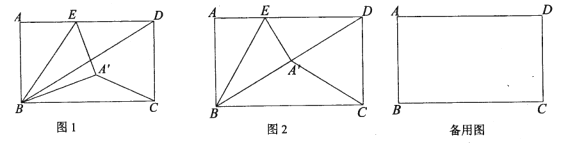
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将![]() 沿弦
沿弦![]() 折叠,使折叠后的劣弧
折叠,使折叠后的劣弧![]() 恰好经过圆心O,连接
恰好经过圆心O,连接![]() 并延长交
并延长交![]() 于点C,点P是优弧
于点C,点P是优弧![]() 上的动点,连接
上的动点,连接![]() .
.
(1)如图,用尺规面出折叠后的劣弧![]() 所在圆的圆心
所在圆的圆心![]() ,并求出
,并求出![]() 的度数;
的度数;
(2)如图,若![]() 是
是![]() 的切线,
的切线,![]() ,求线段
,求线段![]() 的长;
的长;
(3)如图,连接![]() ,过点B作
,过点B作![]() 的重线,交
的重线,交![]() 的延长线于点D,求证:
的延长线于点D,求证:![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,如果一个点的纵坐标恰好是横坐标![]() 倍,那么我们就把这个点定义为“萌点”.
倍,那么我们就把这个点定义为“萌点”.
(1)若点![]() 的坐标分别为
的坐标分别为![]() ,则四边形
,则四边形![]() 四条边上的“萌点”坐标是___.
四条边上的“萌点”坐标是___.
(2)若一次函数![]() 的图像上有一个“萌点”的横坐标是-3,求k值;
的图像上有一个“萌点”的横坐标是-3,求k值;
(3)若二次函数![]() 的图像上没有“萌点”,求k的取值范围.
的图像上没有“萌点”,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】水产经销商以10元/千克的价格收购了1000千克的鳊鱼围养在湖塘中(假设围养期每条鳊鱼的重量保持不变),据市场推测,经过湖塘围养后的鳊鱼的市场价格每围养一天能上涨1元/千克,在围养过程中(最多围养20天),平均每围养一天有10千克的鳊鱼会缺氧浮水。假设对缺氧浮水的鳊鱼能以5元/千克的价格抛售完.
(1)若围养x天后,该水产经销商将活着的鳊鱼一次性出售,加上抛售的缺氧浮水鳊鱼,能获利8500元,则需要围养多少天?
(2)若围养期内,每围养一天需支出各种费用450元,则该水产经销商最多可获利多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】小王、小张和小梅打算各自随机选择本周六的上午或下午去高邮湖的湖上花海去踏青郊游.
(1)小王和小张都在本周六上午去踏青郊游的概率为_______;
(2)求他们三人在同一个半天去踏青郊游的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年3月25日是第二十四个“全国中小学生安全教育日”,某校为加强学生的安全意识,以“防火、防溺水、防食物中毒、防校园欺凌”为主题组织了全校学生参加安全知识竞赛,从中抽取了部分学生成绩(得分为正整数,满分为100分)进行统计,绘制了两幅不完整的统计图,如图所示.
(1)学校共抽取了______名学生,![]() _____,n=______.
_____,n=______.
(2)补全频数直方图;
(3)该校共有2000名学生。若成绩在70分以下(含70分)的学生安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=![]() x2+
x2+![]() x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
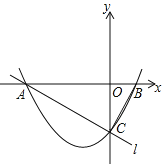
(1)求直线l的解析式;
(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;
(3)取点G(0,-1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO-∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点O是正方形ABCD两条对角线的交点,分别延长CO到点G,OC到点E,使OG=2OD、OE=2OC,然后以OG、OE为邻边作正方形OEFG.
(1)如图1,若正方形OEFG的对角线交点为M,求证:四边形CDME是平行四边形.
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转,得到正方形OE′F′G′,如图2,连接AG′,DE′,求证:AG′=DE′,AG′⊥DE′;
(3)在(2)的条件下,正方形OE′F′G′的边OG′与正方形ABCD的边相交于点N,如图3,设旋转角为α(0°<α<180°),若△AON是等腰三角形,请直接写出α的值.
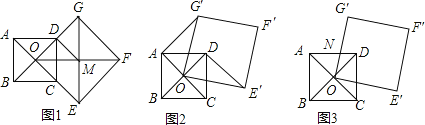
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=90°,E是AC的中点,AE=2.经过点E作△ABE外接圆的切线交BC于点D,过点C作CF⊥BC交BE的延长线于点F,连接FD交AC于点H,FD平分∠BFC.
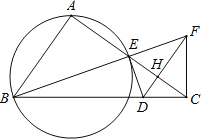
(1)求证:DE=DC;
(2)求证:HE=HC=1;
(3)求BD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com