
科目: 来源: 题型:
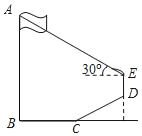
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(结果保留根号).
查看答案和解析>>
科目: 来源: 题型:
【题目】某电器销售商到厂家选购A、B两种型号的液晶电视机,用30000元可购进A型电视10台,B型电视机15台;用30000元可购进A型电视机8台,B型电视机18台.
(1)求A、B两种型号的液晶电视机每台分别多少元?
(2)若该电器销售商销售一台A型液晶电视可获利800元,销售一台B型液晶电视可获利500元,该电器销售商准备用不超过40000元购进A、B两种型号液晶电视机共30台,且这两种液晶电视机全部售出后总获利不低于20400元,问:有几种购买方案?在这几种购买方案中,哪种方案获利最多?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
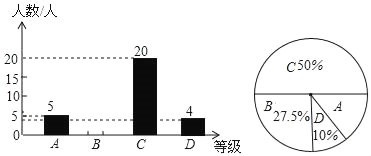
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
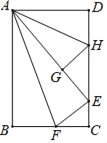
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法:①平方等于其本身的数有0,±1;②32xy3是4次单项式;③将方程![]() 中的分母化为整数,得
中的分母化为整数,得![]() =12;④平面内有4个点,过每两点画直线,可画6条、4条或1条.其中正确的有( )
=12;④平面内有4个点,过每两点画直线,可画6条、4条或1条.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目: 来源: 题型:
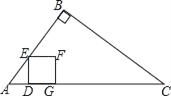
【题目】如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).
(1)求AC的长.
(2)请用含t的代数式表示线段DE的长.
(3)当点F在边BC上时,求t的值.
(4)设正方形DEFG与△ABC重叠部分图形的面积为S(cm2),当重叠部分图形为四边形时,求S与t之间的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,![]() ,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
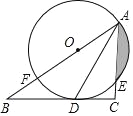
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.
(1)求证:△ADE∽△BEC.
(2)若AD=1,BC=3,AE=2,求AB的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某超市销售一种商品,成本每千克 40 元,规定每千克售价不低于成本,且不高于 80 元,经市场调查,每天的销售量 y( 千克)与每千克售价x(元)满足一次函数关系,部分数据如表:

(1)求 y 与 x 之间的函数表达式;
(2)设商品每天的总利润为 W(元),求 W 与 x 之间的函数表达式(利润=收入﹣成本);
(3)指出售价为多少元时获得利润最大?并试说明(2)中总利润W随售价x的变化而变化的情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com