
科目: 来源: 题型:
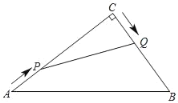
【题目】在Rt△ABC中,∠C=90°,AC=16cm,BC=12cm.现有动点P从点A出发,沿线段AC向点C方向运动,动点Q从点C出发,沿线段CB向点B方向运动.如果点P的速度是4cm/s,点Q的速度是3cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为ts.
求:(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=2s时,P、Q两点之间的距离是多少?
(3)当t为多少秒时,以C、P、Q为顶点的三角形与△ABC相似?
查看答案和解析>>
科目: 来源: 题型:
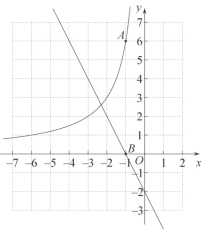
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
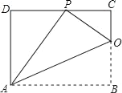
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于点O,连结AP、OP、OA.
(1)求证:△OCP∽△PDA;
(2)若tan∠PAO=![]() ,求边AB的长.
,求边AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
查看答案和解析>>
科目: 来源: 题型:
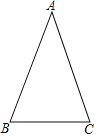
【题目】在△ABC中,AB=AC,∠ABC=70°
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,∠BDC= .
查看答案和解析>>
科目: 来源: 题型:
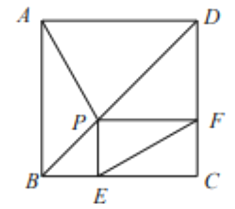
【题目】如图,己知正方形ABCD的边长为4, P是对角线BD上一点,PE⊥BC于点E, PF⊥CD于点F,连接AP, EF.给出下列结论:①PD=![]() EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为
EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为![]() ;⑥AP⊥EF.其中正确结论的序号为( )
;⑥AP⊥EF.其中正确结论的序号为( )
A. ①②④⑤⑥B. ①②④⑤
C. ②④⑤D. ②④⑤⑥
查看答案和解析>>
科目: 来源: 题型:
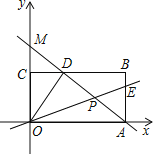
【题目】如图,已知长方形OABC的顶点O在坐标原点,A、C分别在x、y轴的正半轴上,顶点B(8,6),直线y=-x+b经过点A交BC于D、交y轴于点M,点P是AD的中点,直线OP交AB于点E
(1)求点D的坐标及直线OP的解析式;
(2)求△ODP的面积,并在直线AD上找一点N,使△AEN的面积等于△ODP的面积,请求出点N的坐标
(3)在x轴上有一点T(t,0)(5<t<8),过点T作x轴的垂线,分别交直线OE、AD于点F、G,在线段AE上是否存在一点Q,使得△FGQ为等腰直角三角形,若存在,请求出点Q的坐标及相应的t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
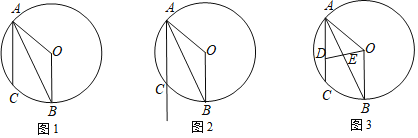
【题目】在圆O中,AO、BO是圆O的半径,点C在劣弧![]() 上,
上,![]() ,
,![]() ,
,![]() ,联结AB.
,联结AB.
![]() 如图1,求证:AB平分
如图1,求证:AB平分![]() ;
;
![]() 点M在弦AC的延长线上,联结BM,如果
点M在弦AC的延长线上,联结BM,如果![]() 是直角三角形,请你在如图2中画出点M的位置并求CM的长;
是直角三角形,请你在如图2中画出点M的位置并求CM的长;
![]() 如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D与点C的距离为x,
如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D与点C的距离为x,![]() 的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.
的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com