
科目: 来源: 题型:
【题目】如图所示,△ABC为Rt△,∠ACB=90°,点D为AB的中点,点E为边AC上的点,连结DE,过点E作EF⊥ED交BC于F,以DE,EF为邻边作矩形DEFG,已知AC=8.
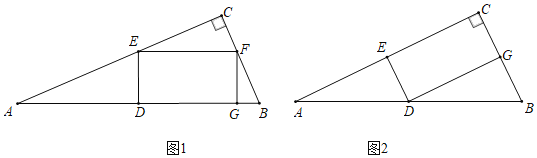
(1)如图1所示,当BC=6,点G在边AB上时,求DE的长.
(2)如图2所示,若![]() ,点G在边BC上时,求BC的长.
,点G在边BC上时,求BC的长.
(3)①若![]() ,且点G恰好落在Rt△ABC的边上,求BC的长.
,且点G恰好落在Rt△ABC的边上,求BC的长.
②若![]() (n为正整数),且点G恰好落在Rt△ABC的边上,请直接写出BC的长.
(n为正整数),且点G恰好落在Rt△ABC的边上,请直接写出BC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】现有一次函数y=mx+n和二次函数y=mx2+nx+1,其中m≠0,
(1)若二次函数y=mx2+nx+1经过点(2,0),(3,1),试分别求出两个函数的解析式.
(2)若一次函数y=mx+n经过点(2,0),且图象经过第一、三象限.二次函数y=mx2+nx+1经过点(a,y1)和(a+1,y2),且y1>y2,请求出a的取值范围.
(3)若二次函数y=mx2+nx+1的顶点坐标为A(h,k)(h≠0),同时二次函数y=x2+x+1也经过A点,已知﹣1<h<1,请求出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
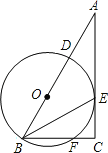
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
查看答案和解析>>
科目: 来源: 题型:
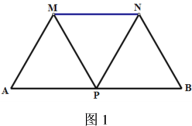
【题目】如图1所示,点P是线段AB的中点,且AB=12,现分别以AP,BP为边,在AB的同侧作等边△MAP和△NBP,连结MN。
(1)请只用不含刻度的直尺在图1中找到△MNP外接圆的圆心O,并保留作图痕迹;
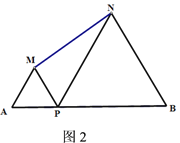
(2)若将“点P是线段AB的中点”改成“点P是线段AB上异于端点的任意一点”,其余条件不变(如图2),请用文字写出△MNP外接圆圆心O的位置,并求出该圆半径的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】小林从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=![]() .然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
.然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.
(1)小明从A点到B点上升的高度是多少米?
(2)小明从A点到C点上升的高度CD是多少米?(结果保留根号)

查看答案和解析>>
科目: 来源: 题型:
【题目】Jack同学寒假去野生动物园游玩,从Baidu地图查找线路发现,几条线路均要换乘,乘车方案如下:在出发站点可选择空调车A,空调车B,普通车a;换乘点可选择空调车C,普通车b,普通车c,所有车辆均在同一站点换乘.
(1)求Jack同学在出发点乘坐空调车的概率;
(2)已知空调车票价2元,普通车票价1元,请用树状图或列表法求Jack同学到达动物园恰好花费3元公交费的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在△ABD中,BC为AD边上的高线,tan∠BAD=1,在BC上截取CG=CD,连结AG,将△ACG绕点C旋转,使点G落在BD边上的F处,A落在E处,连结BE,若AD=4,tanD=3,则△CFD和△ECF的面积比为___;BE长为____.
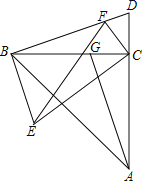
查看答案和解析>>
科目: 来源: 题型:
【题目】将抛物线y1=x2﹣2x﹣3先向左平移1个单位,再向上平移4个单位后,与抛物线y2=ax2+bx+c重合,现有一直线y3=2x+3与抛物线y2=ax2+bx+c相交.当y2≤y3时自变量x的取值范围是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是_______.
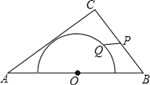
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD,AD=1,CD=2,点P为边CD上的动点(P不与C重合),作点P关于BC的对称点Q,连结AP,BP和BQ,现有两个结论:①若DP≥1,当△APB为等腰三角形时,△APB和△PBQ一定相似;②记经过P,Q,A三点的圆面积为S,则4π≤S<![]() .
.
下列说法正确的是( )
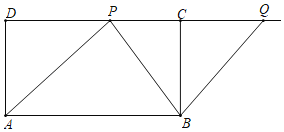
A. ①对②对B. ①对②错C. ①错②对D. ①错②错
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com