
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4(a≠0)与![]() 轴交于点B (-3 ,0) 和C (4 ,0)与
轴交于点B (-3 ,0) 和C (4 ,0)与![]() 轴交于点A.
轴交于点A.
(1) a = ,b = ;
(2) 点M从点A出发以每秒1个单位长度的速度沿AB向B运动,同时,点N从点B出发以每秒1个单位长度的速度沿BC向C运动,当点M到达B点时,两点停止运动.t为何值时,以B、M、N为顶点的三角形是等腰三角形?
(3) 点P是第一象限抛物线上的一点,若BP恰好平分∠ABC,请直接写出此时点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
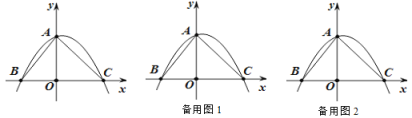
【题目】问题提出:如图1,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP、BP,求AP+![]() BP的最小值.
BP的最小值.
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D,使CD=1,则有![]() ,又∵∠PCD=∠BCP,∴△PCD∽△BCP.∴
,又∵∠PCD=∠BCP,∴△PCD∽△BCP.∴![]() ,∴PD=
,∴PD=![]() BP,∴AP+
BP,∴AP+![]() BP=AP+PD.
BP=AP+PD.
请你完成余下的思考,并直接写出答案:AP+![]() BP的最小值为 .
BP的最小值为 .
(2)自主探索:在“问题提出”的条件不变的情况下,![]() AP+BP的最小值为 .
AP+BP的最小值为 .
(3)拓展延伸:已知扇形COD中,∠COD=90°,OC=6,OA=3,OB=5,点P是![]() 上一点,求2PA+PB的最小值.
上一点,求2PA+PB的最小值.
查看答案和解析>>
科目: 来源: 题型:
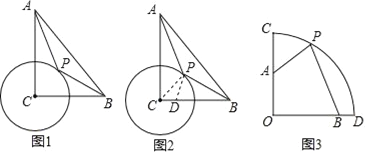
【题目】某网店专门销售某种品牌的学习用品,成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,如图所示.
(1) 求y与x之间的函数关系式;
(2) 当销售单价x为多少元时,每天获取的利润最大,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
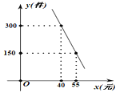
【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动. 对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整). 已知A、B两组捐款户数的比为1 : 5.请结合图中相关数据回答下列问题.
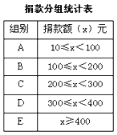
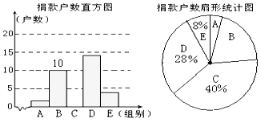
请结合以上信息解答下列问题.
(1) A组捐款户数为 ,本次调查样本的容量是 ;
(2) C组捐款户数为 ,请补全“捐款户数直方图”;
(3) 若该社区有500户住户,请根据以上信息估计,全社区捐款不少于300元的户数是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
(1)CD与⊙O有怎样的位置关系?请说明理由;
(2)若∠CDB=60°,AB=6,求![]() 的长.
的长.
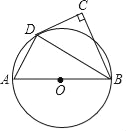
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,4),B(﹣4,n)两点.
的图象交于A(2,4),B(﹣4,n)两点.
(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.
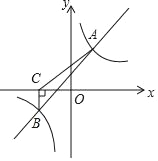
查看答案和解析>>
科目: 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图是二次函数![]() 的图象过点(-1,0),其对称轴为
的图象过点(-1,0),其对称轴为![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④此二次函数的最大值是
;④此二次函数的最大值是![]() ,其中结论正确的是( )
,其中结论正确的是( )
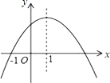
A. ①②B. ②③C. ②④D. ①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
(2) 求证:∠ACF=90°;
(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求![]() 的长.
的长.

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com