
科目: 来源: 题型:
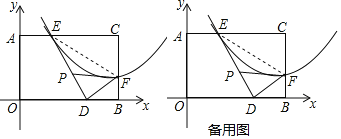
【题目】如图,在平面直角坐标系中,抛物线与矩形AOBC的边AC、BC分别交于点E,F,E(3,4),且F(8,![]() )为抛物线的顶点,将△CEF沿着EF翻折,点C恰好落在边OB上的点D处.
)为抛物线的顶点,将△CEF沿着EF翻折,点C恰好落在边OB上的点D处.
(1)求该抛物线的解析式;
(2)点P为线段ED上一动点,连接PF,当PF平分∠EFD时,求PD的长度;
(3)四边形AODE以1个单位/秒的速度沿着x轴向右运动,当点E与点C重合时停止运动,设运动时间为t秒,运动后的四边形A′O′D′E′与△DEF重合部分的面积为S,请直接写出S与t的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,正△ABC中,点D为BC边的中点,将∠ACB绕点C顺时针旋转α角度(0°<α<60°)得∠A'CB',点P为线段A′C上的一点,连接PD与B′C、AC分别交点点E、F,且∠PAC=∠EDC.
(1)求证:AP=2ED;
(2)猜想PA和PC的位置关系,并说明理由;
(3)如图2,连接AD交B'C于点G,若AP=2,PC=4,求AG的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】深圳某学校为构建书香校园,拟购进甲、乙两种规格的书柜放置新购置的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%,用3600元购进的甲种书柜的数量比用4200元购进的乙种书柜的数量少4台.
(1)求甲、乙两种书柜的进价;
(2)若该校拟购进这两种规格的书柜共60个,其中乙种书柜的数量不大于甲种书柜数量的2倍.请您帮该校设计一种购买方案,使得花费最少.
查看答案和解析>>
科目: 来源: 题型:
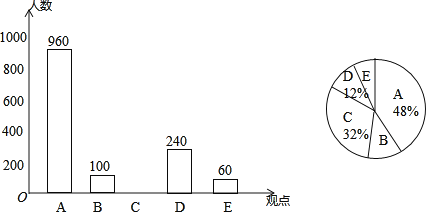
【题目】某公益机构为了解市民使用“手机阅读”的情况,对部分市民进行了随机问卷调查(问卷调查表如左图所示),并将调查结果绘制成两副统计图(均不完整)
您如何看待手机阅读问卷调查表 您好!请在表格中选择一项您最认同的观点,在其后面空格内打“√”,非常感谢您的配合. | ||
选项 | 观点 | 您的选择 |
A | 更新及时 | □ |
B | 阅读成本低 | □ |
C | 不利于人际交往 | □ |
D | 内容丰富 | □ |
E | 其他 | □ |
(1)本次接受调查的总人数是______人.
(2)请将条形统计图补充完整.
(3)在扇形统计图中,表示观点B的扇形的圆心角度数为______度.
(4)根据上述调查结果,请估计在2万名市民中,认为手机阅读“内容丰富“的大约有______人.
查看答案和解析>>
科目: 来源: 题型:
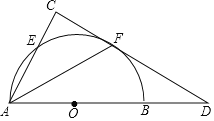
【题目】如图,已知AB是⊙O的直径,⊙O与Rt△ACD的两直角边分别交于点E、F,点F是弧BE的中点,∠C=90°,连接AF.
(1)求证:直线DF是⊙O的切线.
(2)若BD=1,OB=2,求tan∠AFC的值.
查看答案和解析>>
科目: 来源: 题型:
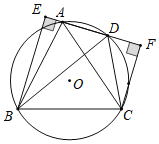
【题目】如图,⊙O是正△ABC的外接圆,点D为圆上一点,连接AD,分别过点B和点C作AD延长线的垂线,垂足分别为点E和点F,连接BD、CD,已知EB=3,FC=2,现在有如下4个结论:①∠CDF=60°;②△EDB∽△FDC;③BC=![]() ;④
;④![]() ,其中正确的结论有( )个
,其中正确的结论有( )个
A. 1
B. 2
C. 3
D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校八年级学生学习《从数据谈节水》后,积极响应“节约用水,从我做起”的号召,下列是10名学生统计各自家族一个月的节水情况:
节水量(m3) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
家族数(个) | 1 | 2 | 2 | 4 | 1 |
那么这组数据的众数和中位数分别是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
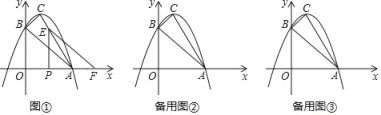
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴的一个交点为A(3,0).与y轴的交点为B(0,3),其顶点为C.
(1)求抛物线的解析式;
(2)将△AOB沿x轴向右平移m个长度单位(0<m<3)后得到另一个△FPE,点A、O、B的像分别为点F、P、E.
①如图①,当点E在直线AC上时,求m的值.
②设所得的三角形△FPE与△ABC重叠部分的面积为S,求S关于m的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
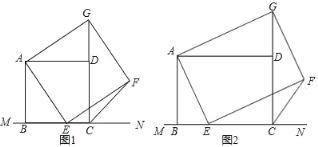
【题目】如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并直接写出∠FCN的度数(不要写出解答过程)
(3)如图(2),将图中正方形ABCD改为矩形ABCD,AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com