
科目: 来源: 题型:
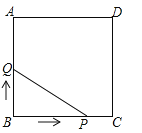
【题目】(3分)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.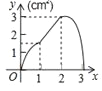 B.
B.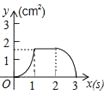 C.
C.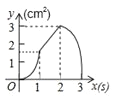 D.
D.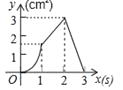
查看答案和解析>>
科目: 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数闭区间[m,n]上的“闭函数”.如函数y=﹣x+4.当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”
(1)反比例函数![]() 是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
(2)若二次函数y=x2﹣2x﹣k是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
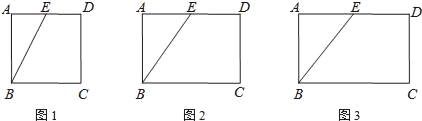
【题目】如图,在矩形ABCD中,E是AD的中点,点A关于BE的对称点为G(G在矩形ABCD内部),连接BG并延长交CD于F.
(1)如图1,当AB=AD时,
①根据题意将图1补全;
②直接写出DF和GF之间的数量关系.
(2)如图2,当AB≠AD时,如果点F恰好为DC的中点,求![]() 的值.
的值.
(3)如图3,当AB≠AD时,如果DC=nDF,写出求![]() 的值的思路(不必写出计算结果).
的值的思路(不必写出计算结果).
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目 选手 | 服装 | 普通话 | 主题 | 演讲技巧 |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
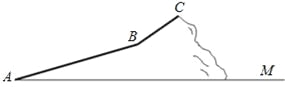
【题目】今年“五一“假期.某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°.已知A点海拔121米.C点海拔721米.
(1)求B点的海拔;
(2)求斜坡AB的坡度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4).动点C从点M(5,0)出发,以1个单位长度/秒的速度沿x轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动,设运动时间为t秒,

(1)请用含t的代数式分别表示出点C与点P的坐标;
(2)以点C为中心,![]() 个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
①当⊙C与射线DE有公共点时,求t的取值范围;
②当△PAB为等腰三角形时,求t的值.
查看答案和解析>>
科目: 来源: 题型:
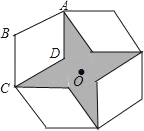
【题目】为了庆祝“六一儿童节”,六年级同学在班会课进行了趣味活动.小舟同学在模板上画出一个菱形ABCD,将它以点O为中心按顺时针方向分别旋转90°,180°,270°后得到如图所示的图形,其中∠ABC=120°,AB=2cm,然后小舟将此图形制作成一个靶子,那么当我们投飞镖时命中阴影部分的概率为( )
A. ![]() B. 2﹣
B. 2﹣![]() C.
C. ![]() -1D.
-1D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将![]() 放在平面直角坐标系中,点
放在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() 动点
动点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以1个单位长度的速度运动,同一时间,动点
以1个单位长度的速度运动,同一时间,动点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以每秒2个单位长度的速度运动,当其中一点到达端点时,另一点也随之停止运动.过点
以每秒2个单位长度的速度运动,当其中一点到达端点时,另一点也随之停止运动.过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() 秒(t
秒(t![]() .
.

(Ⅰ)用含![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅱ)①是否存在![]() 的值,使四边形
的值,使四边形![]() 为平行四边形?若存在,求出
为平行四边形?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
②是否存在![]() 的值,使四边形
的值,使四边形![]() 为菱形?若存在,求出
为菱形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅲ)在整个运动过程中,求出线段![]() 的中点
的中点![]() 所经过的路径长.(直接写出结果即可).
所经过的路径长.(直接写出结果即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】公司有345台电脑需要一次性运送到某学校,计划租用甲、乙两种货车共8辆已知每辆甲种货车一次最多运送电脑45台、租车费用为400元,每辆乙种货车一次最多运送电脑30台、租车费用为280元
(Ⅰ)设租用甲种货车![]() 辆(
辆(![]() 为非负整数),试填写下表.
为非负整数),试填写下表.
表一:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用的甲种货车最多运送电脑的数量/台 | 135 | ||
租用的乙种货车最多运送电脑的数量/台 | 150 |
表二:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用甲种货车的费用/元 | 2800 | ||
租用乙种货车的费用/元 | 280 |
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com