
科目: 来源: 题型:
【题目】直线y=﹣2x+5分别与x轴,y轴交于点C、D,与反比例函数y=![]() 的图象交于点A、B.过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,连结EF;下列结论:①AD=BC;②EF∥AB;③四边形AEFC是平行四边形;④S△EOF:S△DOC=3:5.其中正确的个数是( )
的图象交于点A、B.过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,连结EF;下列结论:①AD=BC;②EF∥AB;③四边形AEFC是平行四边形;④S△EOF:S△DOC=3:5.其中正确的个数是( )
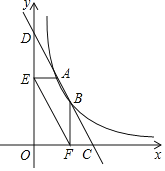
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=26°,则∠OBC的度数为( )
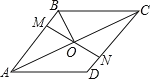
A. 54°B. 64°C. 74°D. 26°
查看答案和解析>>
科目: 来源: 题型:
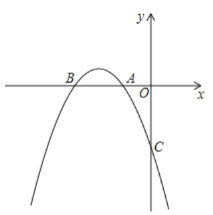
【题目】抛物线y=a(x+2)2+c与x轴交于A,B两点,与y轴负半轴交于点C,已知点A(-1,0),OB=OC.
(1)求此抛物线的解析式;
(2)若把抛物线与直线y=-x-4的交点称为抛物线的不动点,若将此抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点;
(3)Q为直线y=-x-4上一点,在此抛物线的对称轴上是否存在一点P,使得∠APB=2∠AQB,且这样的Q点有且只有一个?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念。
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心。
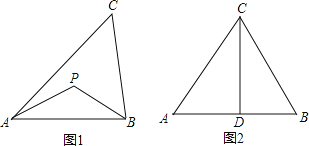
举例:如图1,若PA=PB,则点P为△ABC的准外心。
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=![]() AB,求∠APB的度数。
AB,求∠APB的度数。
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长。
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题情境) 已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
(数学模型)
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(![]() )(x>0)
)(x>0)
(探索研究)
我们可以借鉴以前研究函数的经验,先探索函数y=![]() (x>0)的图象和性质.
(x>0)的图象和性质.
(1)①填写下表,画出函数的图象;


②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=![]() (x>0)的最小值.
(x>0)的最小值.
解决问题:(2)用上述方法解决“问题情境”中的问题,直接写出答案。
查看答案和解析>>
科目: 来源: 题型:
【题目】(2016广东省深圳市)荔枝是深圳的特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)
(1)求桂味和糯米糍的售价分别是每千克多少元;
(2)如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的2倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
科目: 来源: 题型:
【题目】(2013年四川绵阳12分)如图,已知矩形OABC中,OA=2,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.
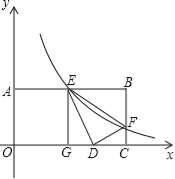
(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
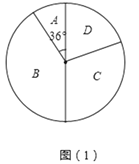
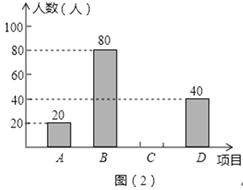
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD=![]() AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的结论是_____.
AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的结论是_____.
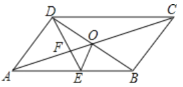
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com