
科目: 来源: 题型:
【题目】2013年12月2日1时30分,中国于西昌卫星发射中心成功将“嫦娥三号”探测器送入轨道.2013年12月15日4时35分,“嫦娥三号”探测器与“玉兔号”月球车分离,“玉兔号”月球车顺利驶抵月球表面,留下了中国在月球上的第一个足迹.“玉兔号”月球车一共在月球上工作了972天,约23000小时.将23000用科学记数法表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某校九(1)班开展数学活动,李明和张华两位同学合作用测角仪测量学校旗杆的高度,李明站在B点测得旗杆顶端E点的仰角为45°,张华站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知李明和张华相距(BD)30米,李明的身高(AB)1.6米,张华的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)

查看答案和解析>>
科目: 来源: 题型:
【题目】定义:经过三角形一边中点,且平分三角形周长的直线叫做这个三角形在该边上的中分线,其中落在三角形内部的部分叫做中分线段.
(1)如图,△ABC中,AC>AB,DE是△ABC在BC边上的中分线段,F为AC中点,过点B作DE的垂线交AC于点G,垂足为H,设AC=b,AB=c.
①求证:DF=EF;
②若b=6,c=4,求CG的长度;
(2)若题(1)中,S△BDH=S△EGH,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
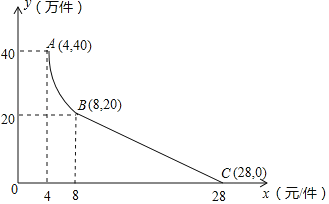
【题目】某公司用100万元研发一种市场急需电子产品,已于当年投入生产并销售,已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,设公司销售这种电子产品的年利润为s(万元).
(1)请求出y(万件)与x(元/件)的函数表达式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)的函数表达式,并求出第一年年利润的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类别,每位同学仅选一项.根据调査结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | a | 0.5 |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | b | 1 |
根据图表提供的信息,回答下列问题:
(1)直接写出:a= .b= m= ;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请求选取的2人恰好是甲和乙的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左、右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等.
(1)(a+b)n展开式中项数共有 项.
(2)写出(a+b)5的展开式:(a+b)5= .
(3)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).
(1)将△ABC沿y轴翻折得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕着点(﹣1,﹣1)旋转180°得到△A2B2C2,画出△A2B2C2;
(3)线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到,直接写出旋转中心的坐标为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC是等腰直角三角形,AB=AC,D为平面内的任意一点,且满足CD=AC,若△ADB是以AD为腰的等腰三角形,则∠CDB的度数为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题背景:在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1:将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD.并且量AB=4cm,AC=8cm,问题解决:
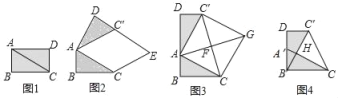
(1)将图1中的△ACD以点为A旋转中心,按逆时针方向能转∠α,使∠α=∠BAC,得到如图2所示的△AC'D,过点C作AC'的平行线,与DC'的延长线交于点E,则四边形ACEC'的形状是 .
(2)缜密小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B、A、D三点在同一条直线上,得到如图3所示的△AC'D,连接CC',取CC'的中点F,连接AF并延长到点G,使FG=AF,连接CG、C'G,得到四边形ACGC',发现它是正方形,请你证明这个结论.
实践探究:(3)创新小组在缜密小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A'点,A'C与BC'相交于点H,如图4所示,连接CC',试求tan∠C'CH的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com