（1）设∠BAD=α，求∠AGE的度数（用含α的代数式表示）；

（2）用等式表示线段CG与BD之间的数量关系，并证明．

（1）求抛物线y=ax2-2ax-3a顶点P的坐标（用含a的代数式表示）；

（2）如果抛物线y=ax2-3ax-3a经过（1，3）．

①求a的值；

②在①的条件下，直接写出“G区域”内整点的个数．

（3）如果抛物线y=ax2-2ax-3a在“G区域”内有4个整点，直接写出a的取值范围．

a．关于“家庭教育”问题发言次数的频数分布直方图如下（数据分成6组：0≤x＜4，4≤x＜8，8≤x＜12，12≤x＜16，16≤x＜20，20≤x≤24）：

b．关于“家庭教育”问题发言次数在8≤x＜12这一组的是：

8899910101010101011111111

c．“面向未来的教育”和“家庭教育”这两问题发言次数的平均数、众数、中位数如下：

根据以上信息，回答下列问题：

（1）表中m的值为______；

（2）在此次采访中，参会教师更感兴趣的问题是______（填“面向未来的教育”或“家庭教育”），理由是______；

（3）假设所有参会教师都接受调查，估计在“家庭教育”这个问题上发言次数超过8次的参会教师有______位．

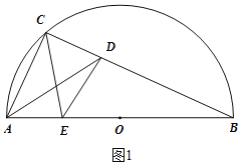
小明根据学习函数经验，分别对函数y1和y2随自变量x变化而变化的规律进行了探究．

下面是小明的探究过程，请将它补充完整：

（1）按表中自变量x值进行取点、画图、测量，得到了y1和y2与x几组对应值：

问题：上表中的m=______cm；

（2）在同一平面直角坐标系xOy中（见图2），描出补全后的表中各组数值所对应的点（x，y2）和（x，y1），并画出函数y1和y2的图象；

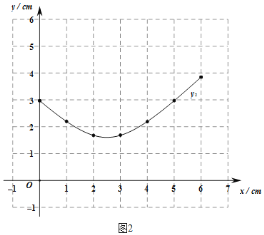
（3）结合函数的图象，解决问题：当△ACE为等腰三角形时，AE的长度约为______cm（结果精确到001）．

（1）求证：BC平分∠DBA；

（2）如果cos∠ABD=，OA=2，求DE的长．

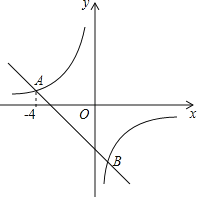
【题目】在平面直角坐标系xOy中，一次函数y=-x+k的图象与反比例函数y=-的图象交于点A（-4，n）和点B．

（1）求k的值和点B的坐标；

（2）若P是x轴上一点，且AP=AB，直接写出点P的坐标．

已知：如图1，线段a和线段b．

求作：△ABC，使得AB=AC，BC=a，BC边上的高为b．

作法：如图2，

①作射线BM，并在射线BM上截取BC=a；

②作线段BC的垂直平分线PQ，PQ交BC于D；

③以D为圆心，b为半径作圆，交PQ于A；

④连接AB和AC．

则△ABC就是所求作的图形．

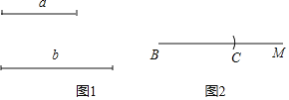
根据上述作图过程，回答问题：

（1）用直尺和圆规，补全图2中的图形；

（2）完成下面的证明：

证明：由作图可知BC=a，AD=b．

∵PQ为线段BC的垂直平分线，点A在PQ上，

∴AB=AC（______）（填依据）．

又∵AD在线段BC的垂直平分线PQ上，

∴AD⊥BC．

∴AD为BC边上的高，且AD=b．

(1)求证：四边形DECF是平行四边形；

(2)若AB＝13，DF＝14，tan A＝，求CF的长．

A. 20B. 35C. 30D. 40