
科目: 来源: 题型:
【题目】有一道作业题:
(1)请你完成这道题的证明;
已知:如图1,在正方形ABCD中,G是对角线BD上一点(G与B,D不重合)连结AG,CG
求证:△BAG≌△BCG
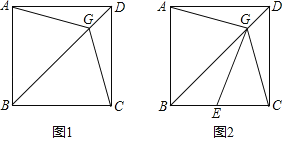
(2)做完(1)后,小颖善于反思,她又提出了如下的问题,请你解答.
如果在射线CB上取点E,使GE=GC,连结GE.
①如图2,当点E在线段CB上时,求证:AG⊥EG.
②探究线段AB,BE,BG之间的数量关系.
查看答案和解析>>
科目: 来源: 题型:
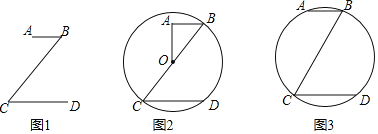
【题目】如图1,有一个“z”字图形,其中AB∥CD,AB:CD:BC=1:2:3.
(1)如图2,若以BC为直径的⊙O恰好经过点D,连结AO.
①求cosC.
②当AB=2时,求AO的长.
(2)如图3,当A,B,C,D四点恰好在同一个圆上时.求∠C的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某人在山坡坡脚C处测得一座建筑物定点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=60m,山坡的坡比为1:2.
(1)求该建筑物的高度(即AB的长,结果保留根号);
(2)求此人所在位置点P的铅直高度(即PD的长,结果保留根号).

查看答案和解析>>
科目: 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

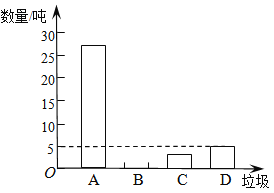
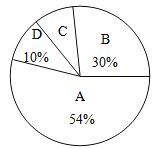
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共 吨;
(3)调查发现,在可回收物中塑料类垃圾占![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠MAN=30°,点B在边AM上,且AB=4![]() ,点P从点A出发沿射线AN方向运动,在边AN上取点C(点C在点P右侧),连结BP,BC.设PC=m,当△BPC成为等腰三角形的个数恰好有3个时,m的值为_____.
,点P从点A出发沿射线AN方向运动,在边AN上取点C(点C在点P右侧),连结BP,BC.设PC=m,当△BPC成为等腰三角形的个数恰好有3个时,m的值为_____.
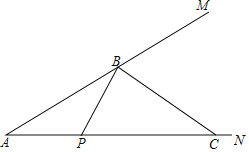
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(4,4),C(﹣2,﹣2),点B,D在反比例函数![]() 的图象上,对角线BD交AC于点M,交x轴于点N,若
的图象上,对角线BD交AC于点M,交x轴于点N,若![]() ,则k的值是_____.
,则k的值是_____.
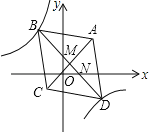
查看答案和解析>>
科目: 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠B=50°,点D为边AB的中点,点E在边AC上,将△ADE沿DE折叠,使得点A恰好落在BC的延长线上的点F处,DF与AC交于点O,连结CD,则下列结论一定正确的是( )
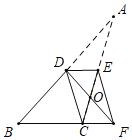
A. CE=EFB. ∠BDF=90°
C. △EOD和△COF的面积相等D. ∠BDC=∠CEF+∠A
查看答案和解析>>
科目: 来源: 题型:
【题目】若抛物线y=ax2+bx+c(a≠0)与x轴两个交点间的距离为6,称此抛物线为定弦抛物线.已知某定弦抛物线开口向上,对称轴为直线x=2,且通过(1,y1),(3,y2),(﹣1,y3),(﹣3,y4)四点,则y1,y2,y3,y4中为正数的是( )
A. y1B. y2C. y3D. y4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在平面直角坐标系中,抛物线y=-![]() x2-
x2-![]() x-3交x轴于A、B两点(点A在点B的左侧),交y轴于点C.
x-3交x轴于A、B两点(点A在点B的左侧),交y轴于点C.

(1)求直线AC的解析式;
(2)①点P是直线AC上方抛物线上的一个动点(不与点A、点C重合),过点P作PD⊥AC于点D,求PD的最大值;
②当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位长度的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒![]() 个单位长度的速度运动到点C停止,当点Q在整个运动过程中用时最少时,求点M的坐标;
个单位长度的速度运动到点C停止,当点Q在整个运动过程中用时最少时,求点M的坐标;
(3)如图②,将△BOC沿直线BC平移,点B平移后的对应点为点B',点O平移后的对应点为点O',点C平移后的对应点为点C',点S是坐标平面内一点,若以A、C、O'、S为顶点的四边形是菱形,求出所有符合条件的点O'的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com