
科目: 来源: 题型:
【题目】某农作物的生长率P与温度t(℃)有如下关系:如图1,当10≤t≤25时可近似用函数![]() 刻画;当25≤t≤37时可近似用函数
刻画;当25≤t≤37时可近似用函数![]() 刻画.
刻画.
(1)求h的值.
(2)按照经验,该作物提前上市的天数m(天)与生长率P满足函数关系:
生长率P | 0.2 | 0.25 | 0.3 | 0.35 |
提前上市的天数m(天) | 0 | 5 | 10 | 15 |
①请运用已学的知识,求m关于P的函数表达式;
②请用含![]() 的代数式表示m ;
的代数式表示m ;
(3)天气寒冷,大棚加温可改变农作物生长速度.在(2)的条件下,原计划大棚恒温20℃时,每天的成本为200元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此给大棚继续加温,加温后每天成本w(元)与大棚温度t(℃)之间的关系如图2.问提前上市多少天时增加的利润最大?并求这个最大利润(农作物上市售出后大棚暂停使用).

查看答案和解析>>
科目: 来源: 题型:
【题目】小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
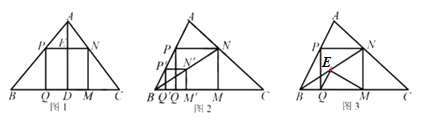
(1)温故:如图1,在△ABC中,AD⊥BC于点D,正方形PQMN的边QM在BC上,顶点P,N分别在AB, AC上,若BC=6,AD=4,求正方形PQMN的边长.
(2)操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结B N′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN.小波把线段BN称为“波利亚线”.
(3)推理:证明图2中的四边形PQMN 是正方形.
(4)拓展:在(2)的条件下,于波利业线B N上截取NE=NM,连结EQ,EM(如图3).当tan∠NBM=![]() 时,猜想∠QEM的度数,并尝试证明.
时,猜想∠QEM的度数,并尝试证明.
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
查看答案和解析>>
科目: 来源: 题型:
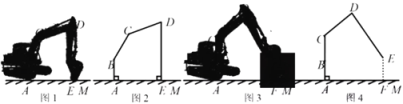
【题目】某挖掘机的底座高AB=0.8米,动臂BC=1.2米,CD=1.5米,BC与CD的固定夹角∠BCD=140°.初始位置如图1,斗杆顶点D与铲斗顶点E所在直线DE垂直地面AM于点E,测得∠CDE=70°(示意图2).工作时如图3,动臂BC会绕点B转动,当点A,B,C在同一直线时,斗杆顶点D升至最高点(示意图4).
(1)求挖掘机在初始位置时动臂BC与AB的夹角∠ABC的度数.
(2)问斗杆顶点D的最高点比初始位置高了多少米(精确到0.1米)?
(考数据:sin50°≈0.77,cos50°≈0.64,sin70°≈0.94,cos70°≈0.34,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】在推进嘉兴市城乡生活垃圾分类的行动中,某社区为了了解居民掌握垃圾分类知识的 情况进行调查.其中A、B 两小区分别有 500 名居民参加了测试,社区从中各随机 抽取50 名居民成绩进行整理得到部分信息:
(信息一)A 小区 50 名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值):
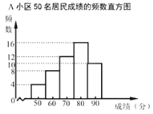
(信息二)上图中,从左往右第四组的成绩如下

(信息三)A、B 两小区各 50 名居民成绩的平均数、中位数、众数、优秀率(80 分及以上为优秀)、方差等数据如下(部分空缺):

根据以上信息,回答下列问题:
(1)求A 小区 50 名居民成绩的中位数.
(2)请估计A 小区 500 名居民成绩能超过平均数的人数.
(3)请尽量从多个角度,选择合适的统计量分析 A,B 两小区参加测试的居民掌握垃圾分类知识的情况.
查看答案和解析>>
科目: 来源: 题型:
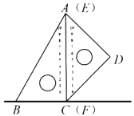
【题目】如图,一副含30°和45°角的三角板ABC和EDF拼合在个平面上,边AC与EF重合,AC=12cm.当点E从点A出发沿AC方向滑动时,点F同时从点C出发沿射线BC方向滑动.当点E从点A滑动到点C时,点D运动的路径长为__cm;连接BD,则△ABD的面积最大值为___cm2.
查看答案和解析>>
科目: 来源: 题型:
【题目】小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与![]() 轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年5月26日第5届中国国际大数据产业博览会召开.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是( )

A. 签约金额逐年增加
B. 与上年相比,2019年的签约金额的增长量最多
C. 签约金额的年增长速度最快的是2016年
D. 2018年的签约金额比2017年降低了22.98%
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,已知P(x1,y1)Q(x2,y2),定义P、Q两点的横坐标之差的绝对值与纵坐标之差的绝对值的和为P、Q两点的直角距离,记作d(P,Q).即d(P,Q)=|x2﹣x1|+|y2﹣y1|
如图1,在平面直角坐标系xOy中,A(1,4),B(5,2),则d(A,B)=|5﹣1|+|2﹣4|=6.
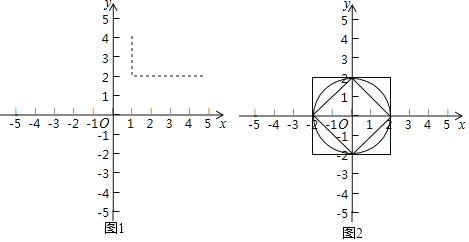
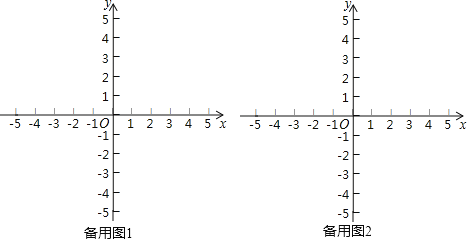
(1)如图2,已知以下三个图形:
①以原点为圆心,2为半径的圆;
②以原点为中心,4为边长,且各边分别与坐标轴垂直的正方形;
③以原点为中心,对角线分别在两条坐标轴上,对角线长为4的正方形.
点P是上面某个图形上的一个动点,且满足d(O,P)=2总成立.写出符合题意的图形对应的序号 .
(2)若直线y=k(x+3)上存在点P使得d(O,P)=2,求k的取值范围.
(3)在平面直角坐标系xOy中,P为动点,且d(O,P)=3,⊙M圆心为M(t,0),半径为1.若⊙M上存在点N使得PN=1,求t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com