
科目: 来源: 题型:
【题目】如图①,在矩形ABCD中,AB>AD,对角线AC、BD相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动,设点P的运动路径为x,△AOP的面积为y,图②是y关于x的函数关系图象,则AB边的长为( )
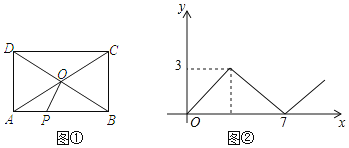
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以矩形ABOD的两边OD、OB为坐标轴建立直角坐标系,若E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交OD于F点.若OF=I,FD=2,则G点的坐标为( )
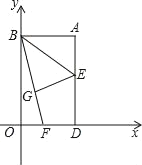
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,按以下步骤作图:①分别以点
,按以下步骤作图:①分别以点![]() 和点
和点![]() 为圆心,为圆心,大于号
为圆心,为圆心,大于号![]() 的长为半径面狐,两弧交于点
的长为半径面狐,两弧交于点![]() ,
,![]() :②做直线
:②做直线![]() ,且
,且![]() 恰好经过点
恰好经过点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,我们将相同的两块含30°角的直角三角板Rt△DEF与Rt△ABC叠合,使DE在AB上,DE过点C,已知AC=DE=6.
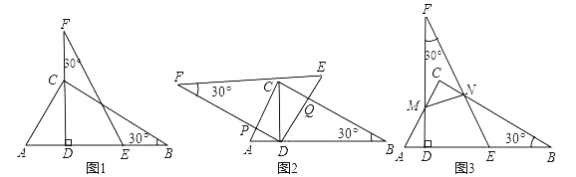
(1)将图1中的△DEF绕点D逆时针旋转(DF与AB不重合),使边DF、DE分别交AC、BC于点P、Q,如图2.
①求证:△CQD∽△APD;②连接PQ,设AP=x,求面积S△PCQ关于x的函数关系式;
(2)将图1中的△DEF向左平移(点A、D不重合),使边FD、FE分别交AC、BC于点M、N设AM=t,如图3.
①判断△BEN是什么三角形?并用含t的代数式表示边BE和BN;②连接MN,求面积S△MCN关于t的函数关系式;
(3)在旋转△DEF的过程中,试探求AC上是否存在点P,使得S△PCQ等于平移所得S△MCN的最大值?说明你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,∠OAB=90°且OA=AB,OB=8,OC=5.
(1)求点A的坐标;
(2)点P是从O点出发,沿X轴正半轴方向以每秒1单位长度的速度运动至点B的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,交四边形ABCD的边AO或AB于点Q,交OC或BC于点R.设运动时间为t(s),已知t=3时,直线l恰好经过点 C.
求①点P出发时同时点E也从点B出发,以每秒1个单位的速度向点O运动,点P停止时点E也停止.设△QRE的面积为S,求当0<t<3时S与t的函数关系式;并直接写出S的最大值.
②是否存在某一时刻t,使得△ORE为直角三角形?若存在,请求出相应t的值;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
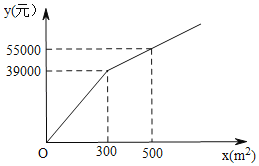
【题目】为了美化环境,建设宜居衡阳,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)求y与x的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1000m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的3倍,那么应该怎忙分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目: 来源: 题型:
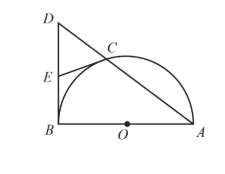
【题目】如图,AB 为半⊙O 的直径,弦 AC 的延长线与过点 B 的切线交于点 D,E 为 BD的中点,连接 CE.
(1)求证:CE 为 O 的切线;
(2)过点 C 作 CF AB ,垂足为点 F,AC=5,CF=3,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
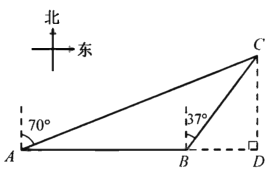
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,诵读经典”活动,学习随机抽查了部分学生,对他们每天的课外阅读时间进行调查,并将调查统计的结果分为四类:每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟记为B类,40分钟<t≤60分钟记为C类,t>60分钟记为D类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)这次共抽取了 名学生进行调查统计,扇形统计图中D类所对应的扇形圆心角大小为 ;
(2)将条形统计图补充完整;
(3)如果该校共有2000名学生,请你估计该校C类学生约有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于点A、B,抛物线
轴分别交于点A、B,抛物线![]() 经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0﹤t﹤5.
经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0﹤t﹤5.

(1)求抛物线的解析式;
(2)当t为何值时,以A、D、E为顶点的三角形与△AOB相似;
(3)当△ADE为等腰三角形时,求t的值;
(4)抛物线上是否存在一点F,使得以A、B、D、F为顶点的四边形是平行四边形?若存在,直接写出F点的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com