
科目: 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() .
.
(1)如图1,已知![]() 经过点
经过点![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]() ,求
,求![]() 的直径长;
的直径长;
(2)如图2,已知直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和点
和点![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点,以
上的一个动点,以![]() 为圆心,
为圆心,![]() 为半径画圆.
为半径画圆.
①当点![]() 与点
与点![]() 重合时,求证: 直线
重合时,求证: 直线![]() 与
与![]() 相切;
相切;
②设![]() 与直线
与直线![]() 相交于
相交于![]() 两点, 连结
两点, 连结![]() . 问:是否存在这样的点
. 问:是否存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,若存在,求出点
是等腰直角三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
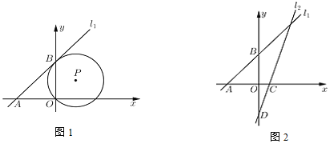
查看答案和解析>>
科目: 来源: 题型:
【题目】某校的甲、乙两位老师同住一小区,该小区与学校相距2400米. 甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校义骑行若干米到达还车点后,立即步行走回学校. 已知甲步行的速度比乙步行的速度每分钟快5米. 设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 和折线
和折线![]() 分别表示甲、乙离开小区的路程
分别表示甲、乙离开小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)在图2中,画出当![]() 时
时![]() 关于
关于![]() 的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)

查看答案和解析>>
科目: 来源: 题型:
【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |
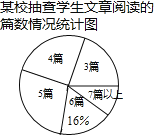
请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度. 图2是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=![]() . 若AO=85cm,BO=DO=65cm. 问: 当
. 若AO=85cm,BO=DO=65cm. 问: 当![]() ,较长支撑杆的端点
,较长支撑杆的端点![]() 离地面的高度
离地面的高度![]() 约为_____
约为_____![]() .(参考数据:
.(参考数据:![]()
![]() ,
,![]() .)
.)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,![]() 经过等边
经过等边![]() 的顶点
的顶点![]() ,
,![]() (圆心
(圆心![]() 在
在![]() 内),分别与
内),分别与![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,
,![]() ,连结
,连结![]() ,
,![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() .
.
(2)当![]() ,
,![]() 时,求
时,求![]() 的长。
的长。
(3)设![]() ,
,![]() .
.
①求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
②如图2,连结![]() ,
,![]() ,若
,若![]() 的面积是
的面积是![]() 面积的10倍,求
面积的10倍,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
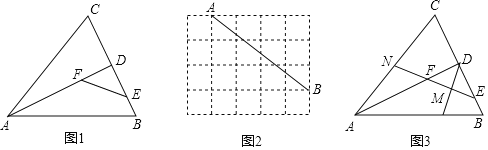
(1)如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点.求证:四边形
上的点.求证:四边形![]() 是邻余四边形.
是邻余四边形.
(2)如图2,在![]() 的方格纸中,
的方格纸中,![]() ,
,![]() 在格点上,请画出一个符合条件的邻余四边形
在格点上,请画出一个符合条件的邻余四边形![]() ,使
,使![]() 是邻余线,
是邻余线,![]() ,
,![]() 在格点上.
在格点上.
(3)如图3,在(1)的条件下,取![]() 中点
中点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .若
.若![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,求邻余线
,求邻余线![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图2所示.
(分)的函数关系如图2所示.

(1)求第一班车离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数表达式.
(分)的函数表达式.
(2)求第一班车从人口处到达塔林所蓄的时间.
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聘聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
查看答案和解析>>
科目: 来源: 题型:
【题目】今年5月15日,亚洲文明对话大会在北京开幕.为了增进学生对亚洲文化的了解,某学校开展了相关知识的宣传教育活动。为了解这次宣传活动的效果,学校从全校1200名学生中随机抽取100名学生进行知识测试(测试满分100分,得分均为整数),并根据这100人的测试成绩,制作了如下统计图表。
100名学生知识测试成绩的频数表
成绩 | 频数(人) |
| 10 |
| 15 |
|
|
| 40 |
| 15 |
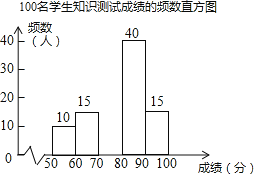
由图表中给出的信息回答下列问题:
(1)![]() ________,并补全额数直方图________;
________,并补全额数直方图________;
(2)小明在这次测试中成绩为85分,你认为85分一定是这100名学生知识测试成绩的中位数吗?请简要说明理由;
(3)如果80分以上(包括80分)为优秀,请估计全校1200名学生中成绩优秀的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com