
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.

(1)求抛物线的表达式;
(2)写出点![]() 的坐标并求直线
的坐标并求直线![]() 的表达式;
的表达式;
(3)设动点![]() ,
,![]() 分别在抛物线和对称轴l上,当以
分别在抛物线和对称轴l上,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() ,
,![]() 两点的坐标.
两点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目: 来源: 题型:
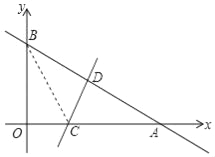
【题目】如图,已知直线y=﹣![]() x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ;点B的坐标为 ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)直线BC上是否存在一点M,使得△ABM的面积与△ABO的面积相等?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象.
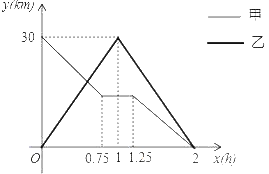
(1)A、B两地间的距离为 km;
(2)求乙与B地的距离y(km)与乙行驶时间x(h)之间的函数关系式;
(3)求甲、乙第一次相遇的时间;
(4)若两人之间的距离不超过10km时,能够用无线对讲机保持联系,请求出乙在行进中能用无线对讲机与甲保持联系的x取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】调查作业:了解你所住小区家庭3月份用气量情况
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2~5之间,这300户家庭的平均人数约为3.3.
小天、小东、小芸各自对该小区家庭3月份用气量情况进行了抽样裯查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1抽样调查小区4户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以|材料回答问题:
(1)小天、小东和小芸三人中,哪位同学抽样调查的数据能较好地反映出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处.
(2)在表3中,调查的15个家庭中使用气量的中位数是 m3,众数是 m3.
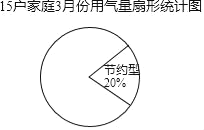
(3)小东将表2中的数据按用气量x(m3)大小分为三类.
①节约型:10≤x≤13,②适中型:14≤x≤17,③偏高型:18≤x≤22,并绘制成如图扇形统讣图,请帮助他将扇形图补充完整.
(4)小芸算出表3中3月份平均每人的用气量为6m3,请估计该小区3月份的总用气量.
查看答案和解析>>
科目: 来源: 题型:
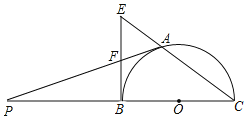
【题目】如图,BC是半⊙O的直径,A是⊙O上一点,过点的切线交CB的延长线于点P,过点B的切线交CA的延长线于点E,AP与BE相交于点F.
(1)求证:BF=EF;
(2)若AF=![]() ,半⊙O的半径为2,求PA的长度.
,半⊙O的半径为2,求PA的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目: 来源: 题型:
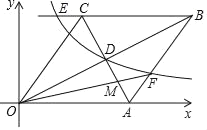
【题目】如图,菱形OABC,A点的坐标为(5,0),对角线OB、AC相交于D点,双曲线y=![]() (x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OBAC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6
(x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OBAC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6![]() ;④S△AFM:S△AOM=1:3.其中正确的结论是( )
;④S△AFM:S△AOM=1:3.其中正确的结论是( )
A. ①②B. ①③C. ①②③D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
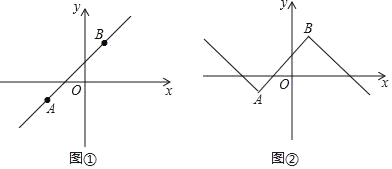
【题目】已知:在平面直角坐标系xOy中,点A(x1,y1)、B(x2,y2)是某函数图象上任意两点(x1<x2),将函数图象中x<x1的部分沿直线y=y1作轴对称,x>x2的部分沿直线y=y2作轴对称,与原函数图象中x1≤x≤x2的部分组成了一个新函数的图象,称这个新函数为原函数关于点A、B的“双对称函数”.例如:如图①,点A(﹣2,﹣1)、B(1,2)是一次函数y=x+1图象上的两个点,则函数y=x+1关于点A、B的“双对称函数”的图象如图②所示.
(1)点A(t,y1)、B(t+3,y2)是函数y=![]() 图象上的两点,y=
图象上的两点,y=![]() 关于点A、B的“双对称函数”的图象记作G,若G是中心对称图形,直接写出t的值.
关于点A、B的“双对称函数”的图象记作G,若G是中心对称图形,直接写出t的值.
(2)点P(![]() ,y1),Q(
,y1),Q(![]() +t,y2)是二次函数y=(x﹣t)2+2t图象上的两点,该二次函数关于点P、Q的“双对称函数”记作f.
+t,y2)是二次函数y=(x﹣t)2+2t图象上的两点,该二次函数关于点P、Q的“双对称函数”记作f.
①求P、Q两点的坐标(用含t的代数式表示).
②当t=﹣2时,求出函数f的解析式;
③若﹣1≤x≤1时,函数f的最小值为ymin,求﹣2≤ymin≤﹣1时,t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1:在平面直角坐标系内,O为坐标原点,线段AB两端点在坐标轴上且点A(﹣4,0),点B(0,3),将AB向右平移4个单位长度至OC的位置
(1)直接写出点C的坐标 ;
(2)如图2,过点C作CD⊥x轴于点D,在x轴正半轴有一点E(1,0),过点E作x轴的垂线,在垂线上有一动点P,直接写出:①点D的坐标 ; ②三角形PCD的面积为 ;
(3)如图3,在(2)的条件下,连接AC,当△ACP的面积为![]() 时,直接写出点P的坐标 .
时,直接写出点P的坐标 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com