
科目: 来源: 题型:
【题目】y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是( )
A. a≤﹣5B. a≥5C. a=7D. a≥7
查看答案和解析>>
科目: 来源: 题型:
【题目】以下说法合理的是( )
A. 小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是![]()
B. 某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C. 某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是![]()
D. 小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是![]()
查看答案和解析>>
科目: 来源: 题型:
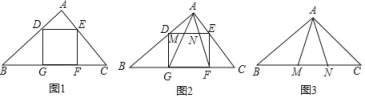
【题目】(1)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,若AB=AC=2,求DE的长;
(2)如图,在(1)的条件下,连结AG、AF分别交DE于M、N两点,求MN的长;
(3)如图,在△ABC中,AB=AC=BN=2,∠BAC=108°,若AM=AN,请直接写出MN的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一张长方形纸片,AB=CD=a,AD=BC=b(a<b<2a).
将这张纸片沿着过点A的折痕翻折,使点B落在AD边上的点F,折痕交BC于点E,将折叠后的纸片再次沿着另一条过点A的折痕翻折,点E恰好与点D重合,此时折痕交DC于点G.
(1)在图中确定点F、点E和点G的位置;
(2)连接AE,则∠EAB= °;
(3)用含有a、b的代数式表示线段DG的长.

查看答案和解析>>
科目: 来源: 题型:
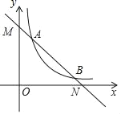
【题目】如图,在平面直角坐标中,点O是坐标原点,一次函数y1=kx+b与反比例函数y2=![]() (x>0)的图象交于A(1,m)、B(n,1)两点.
(x>0)的图象交于A(1,m)、B(n,1)两点.
(1)求直线AB的解析式及△OAB面积;
(2)根据图象写出当y1<y2时,x的取值范围;
(3)若点P在x轴上,求PA+PB的最小值.
查看答案和解析>>
科目: 来源: 题型:
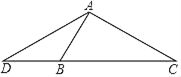
【题目】如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连结AB,且有AB=DB.
(1)求证:△ADB∽△CDA;
(2)若DB=2,BC=3,求AD的值.
查看答案和解析>>
科目: 来源: 题型:
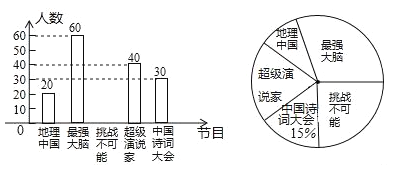
【题目】我市某中学为了了解孩子们对《中国诗词大会》、《挑战不可能》、《最强大脑》、《超级演说家》、《地理中国》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:
(1)本次调查中共抽取了 名学生.
(2)补全条形统计图.
(3)在扇形统计图中,喜爱《地理中国》节目的人数所在的扇形的圆心角是 度.
查看答案和解析>>
科目: 来源: 题型:
【题目】浙江实施“五水共治“以来,越来越重视节约用水,某地对居民用水按阶梯水价方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元),请根据图象信息,回答下列问题.
(1)请写出y与x的函数关系式;
(2)若某个家庭有5人,响应节水号召,计划控制1月份的生活用水费不超过76元,则该家庭这个月最多可以用多少吨水?
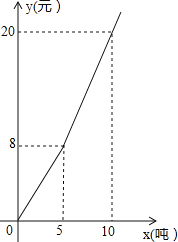
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在△ABC中,AB=AC,AD⊥BC,垂足为点D,以AD为对角线作正方形AEDF,DE交AB于点M,DF交AC于点N,连结EF,EF分别交AB、AD、AC于点G、点O、点H.
(1)求证:EG=HF;
(2)当∠BAC=60°时,求![]() 的值;
的值;
(3)设![]() ,△AEH和四边形EDNH的面积分别为S1和S2,求
,△AEH和四边形EDNH的面积分别为S1和S2,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,函数y1=ax+b(a、b为常数,且ab≠0)的图象如图所示,y2=bx+a,设y=y1·y2.
(1)当b=-2a时,
①若点(1,4)在函数y的图象上,求函数y的表达式;
②若点(x1,p)和(x2,q)在函数y的图象上,且![]() ,比较p,q的大小;
,比较p,q的大小;
(2)若函数y的图象与x轴交于(m,0)和(n,0)两点,求证:m=![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com