
科目: 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲![]() 如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元
如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元![]() 为整数
为整数![]() .
.
![]() 直接写出每天游客居住的房间数量y与x的函数关系式.
直接写出每天游客居住的房间数量y与x的函数关系式.
![]() 设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
![]() 某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人
某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人![]() 问:这天宾馆入住的游客人数最少有多少人?
问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
科目: 来源: 题型:
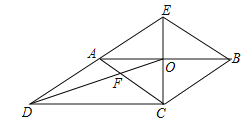
【题目】如图,CE是ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四边形AFOE:S△COD=2:3.
其中正确的结论有_____.(填写所有正确结论的序号)
查看答案和解析>>
科目: 来源: 题型:
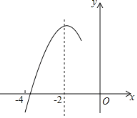
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示.则下列结论:①
之间,其部分图象如图所示.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤点
为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ,正确的个数有( )
,正确的个数有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】对于二次函数![]() 和一次函数
和一次函数![]() ,我们把
,我们把 ![]() 称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n),请完成下列任务:
称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n),请完成下列任务:
(尝试)
(1)当t=2时,抛物线![]() 的顶点坐标为 .
的顶点坐标为 .
(2)判断点A是否在抛物线E上;
(3)求n的值.
(发现)通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,定点的坐标 .
(应用)二次函数![]() 是二次函数
是二次函数![]() 和一次函数
和一次函数 ![]() 的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在三角形ABC中,∠ACB=90°,AC=6,BC=8,点D为边BC的中点,射线DE⊥BC交AB于点E.点P从点D出发,沿射线DE以每秒1个单位长度的速度运动.以PD为斜边,在射线DE的右侧作等腰直角△DPQ.设点P的运动时间为t(秒).
(1)用含t的代数式表示线段EP的长.
(2)求点Q落在边AC上时t的值.
(3)当点Q在△ABC内部时,设△PDQ和△ABC重叠部分图形的面积为S(平方单位),求S与t之间的函数关系式.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】中华文化历史悠久,包罗万象.某校为了加强学生对中华传统文化的认识和理解,营造校园文化氛围,举办了“弘扬中华传统文化,做新时代的中学生”的知识竞赛.以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
七年级: 76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
八年级: 74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
(1)根据上面的数据,将下列表格补充完整,整理、描述数据:
|
|
|
|
| |
七年级 | 1 | 2 | 6 | ||
八年级 | 0 | 1 | 10 | 1 | 8 |
(说明:成绩90分及以上为优秀,60分以下为不合格)分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 84 | 88.5 | |
八年级 | 84.2 | 74 |
(2)为调动学生学习传统文化的积极性,七年级根据学生的成绩制定了奖励标准,凡达到或超过这个标准的学生将获得奖励.如果想让一半左右的学生能获奖,应根据______来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”);
(3)若八年级有800名学生,试估计八年级学生成绩优秀的人数;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数![]() 的图象过点
的图象过点![]() 和点
和点![]() ,对称轴为直线
,对称轴为直线![]() .
.

![]() 求该二次函数的关系式和顶点坐标;
求该二次函数的关系式和顶点坐标;
![]() 结合图象,解答下列问题:
结合图象,解答下列问题:
①当![]() 时,求函数
时,求函数![]() 的取值范围.
的取值范围.
②当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com