
科目: 来源: 题型:
【题目】小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与![]() 轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目: 来源: 题型:
【题目】在公园有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为![]() 公分.敏敏观察到高度
公分.敏敏观察到高度![]() 公分矮圆柱的影子落在地面上,其影长为
公分矮圆柱的影子落在地面上,其影长为![]() 公分;而高圆柱的部分影子落在墙上,如图所示.
公分;而高圆柱的部分影子落在墙上,如图所示.

已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
(1)若敏敏的身高为![]() 公分,且此刻她的影子完全落在地面上,则影长为多少公分?
公分,且此刻她的影子完全落在地面上,则影长为多少公分?
(2)若同一时间量得高圆柱落在墙上的影长为![]() 公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
公分,则高圆柱的高度为多少公分?请详细解释或完整写出你的解题过程,并求出答案.
查看答案和解析>>
科目: 来源: 题型:
【题目】市面上贩售的防晒产品标有防晒指数![]() ,而其对抗紫外线的防护率算法为:防护率
,而其对抗紫外线的防护率算法为:防护率![]() ,其中
,其中![]() .
.
请回答下列问题:
(1)厂商宣称开发出防护率![]() 的产品,请问该产品的
的产品,请问该产品的![]() 应标示为多少?
应标示为多少?
(2)某防晒产品文宣内容如图所示.
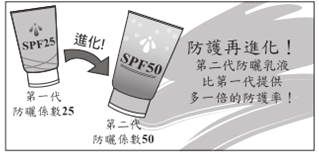
请根据![]() 与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
查看答案和解析>>
科目: 来源: 题型:
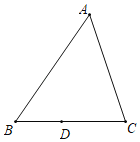
【题目】如图的![]() 中,
中,![]() ,且
,且![]() 为
为![]() 上一点.今打算在
上一点.今打算在![]() 上找一点
上找一点![]() ,在
,在![]() 上找一点
上找一点![]() ,使得
,使得![]() 与
与![]() 全等,以下是甲、乙两人的作法:
全等,以下是甲、乙两人的作法:
(甲)连接![]() ,作
,作![]() 的中垂线分别交
的中垂线分别交![]() 、
、![]() 于
于![]() 点、
点、![]() 点,则
点,则![]() 、
、![]() 两点即为所求
两点即为所求
(乙)过![]() 作与
作与![]() 平行的直线交
平行的直线交![]() 于
于![]() 点,过
点,过![]() 作与
作与![]() 平行的直线交
平行的直线交![]() 于
于![]() 点,则
点,则![]() 、
、![]() 两点即为所求
两点即为所求
对于甲、乙两人的作法,下列判断何者正确?( )
A. 两人皆正确B. 两人皆错误
C. 甲正确,乙错误D. 甲错误,乙正确
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示A、B、C、D四点在⊙O上的位置,其中![]() =180°,且
=180°,且![]() =
=![]() ,
,![]() =
=![]() .若阿超在
.若阿超在![]() 上取一点P,在
上取一点P,在![]() 上取一点Q,使得∠APQ=130°,则下列叙述何者正确( )
上取一点Q,使得∠APQ=130°,则下列叙述何者正确( )

A. Q点在![]() 上,且
上,且![]() >
>![]() B. Q点在
B. Q点在![]() 上,且
上,且![]() <
<![]()
C. Q点在![]() 上,且
上,且![]() >
>![]() D. Q点在
D. Q点在![]() 上,且
上,且![]() <
<![]()
查看答案和解析>>
科目: 来源: 题型:
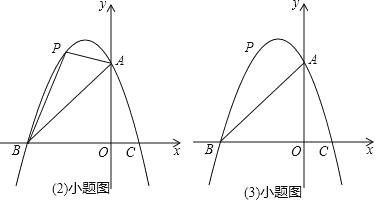
【题目】已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好,并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次研究中,一共调查了 名学生;若该校共有![]() 名学生,估计全校爱好运动的学生共有 名;
名学生,估计全校爱好运动的学生共有 名;
(2)补全条形统计图,并计算阅读部分圆心角是 ;
(3)在全校同学中随机选出一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生概率是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()
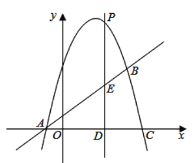
(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com