
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.
(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.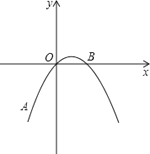
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() .
.
(1)该抛物线的对称轴是直线___________,顶点坐标是___________;
(2)选取适当的数据填入下表,并在图中的直角坐标系内画出该抛物线的图像;


(3)根据图像回答,![]() 有实数根,此时
有实数根,此时![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
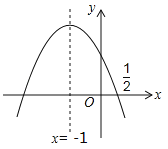
【题目】(4分)如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】图(1)所示矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 满足的反比例函数关系如图(2)所示,等腰直角三角形
满足的反比例函数关系如图(2)所示,等腰直角三角形![]() 的斜边
的斜边![]() 过点
过点![]() ,
,![]() 为
为![]() 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )

A. 当![]() 时,
时,![]()
B. 当![]() 时,
时,![]()
C. 当![]() 增大时,
增大时,![]() 的值增大
的值增大
D. 当![]() 增大时,
增大时,![]() 的值不变
的值不变
查看答案和解析>>
科目: 来源: 题型:
【题目】在一堂数学实践课上,赵老师给出了下列问题:
(提出问题)
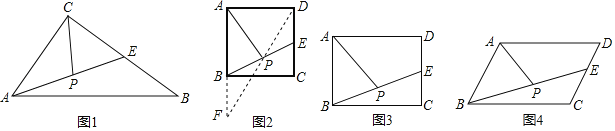
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5.则CP= .
(探究规律)
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为 (按图示辅助线求解);
(3)在图3中,AP是矩形ABCD的“双中线”,若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(拓展应用)
(4)在图4中,AP是平行四边形ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°.求出△ABP的周长,并说明理由?
查看答案和解析>>
科目: 来源: 题型:
【题目】小琴的父母承包了一块荒山地种植一批梨树,今年收获一批金溪密梨,小琴的父母打算以m元/斤的零售价销售5000斤密梨;剩余的5000(m+1)斤密犁以比零售价低1元的批发价批给外地客商,预计总共可赚得55 000元的毛利润.

(1)求小琴的父母今年共收获金溪密梨多少斤?
(2)若零售金溪密梨平均每天可售出200斤,每斤盈利2元.为了加快销售和获得较好的售价,采取了降价措施,发现销售单价每降低0.1元,平均每天可多售出40斤,应降价多少元?每天销售利润为600元.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在□ABCD中,AB=2cm,线段AB与直线l之间的距离为![]() cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
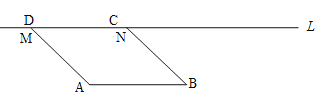
(1)当t=____s时,□ABCD为矩形;
(2)线段CD在直线l上移动过程中,当□ABCD为菱形时,求线段CD运动时间t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com