
科目: 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列说法中,正确的是( )
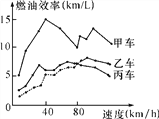
A. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
B. 以低于80 km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少
C. 以高于80 km/h的速度行驶时,行驶相同路程,丙车比乙车省油
D. 以80 km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升
查看答案和解析>>
科目: 来源: 题型:
【题目】我们规定抛物线![]() 与
与![]() 轴有两个不同的交点
轴有两个不同的交点![]() ,
,![]() 时,线段
时,线段![]() 称为该抛物线的“横截弦”,其长度记为
称为该抛物线的“横截弦”,其长度记为![]() .
.
(1)已知抛物线![]() ,则
,则![]() ;
;
(2)已知抛物线![]() 经过点
经过点![]() ,当
,当![]() 时,求该抛物线所对应的函数解析式;
时,求该抛物线所对应的函数解析式;
(3)已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
①抛物线恒存在“横截弦”,求![]() 的取值范围;
的取值范围;
②求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
③连接![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 时,请直接写出
时,请直接写出![]() 取值范围.
取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 以
以![]() 的速度运动,同时动点
的速度运动,同时动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 以
以![]() 的速度向终点
的速度向终点![]() 运动,以
运动,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .设平行四边形
.设平行四边形![]() 与直角三角形
与直角三角形![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 运动的时间为
运动的时间为![]() .
.
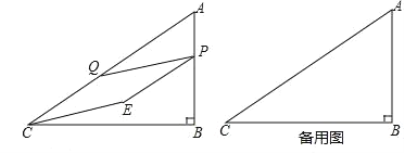
(1)当点![]() 落在线段
落在线段![]() 上时,求
上时,求![]() 的值;
的值;
(2)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当四边形![]() 为矩形时,直接写出
为矩形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角三角形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.

(1)判断![]() 的形状为 ;
的形状为 ;
(2)当![]() 时,求证四边形
时,求证四边形![]() 为正方形;
为正方形;
(3)若![]() ,连接
,连接![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】假期小颖决定到游泳馆游泳,游泳馆门票有两种:![]() 种是每天购票进馆,没有优惠;
种是每天购票进馆,没有优惠;![]() 种是每月先购买贵宾卡,持贵宾卡购票每张可减少8元.设小颖游泳
种是每月先购买贵宾卡,持贵宾卡购票每张可减少8元.设小颖游泳![]() 次,
次,![]() (元)是按
(元)是按![]() 种购票方案的费用,
种购票方案的费用,![]() (元)是按
(元)是按![]() 种购票方案的费用根据图中信息解答问题:
种购票方案的费用根据图中信息解答问题:
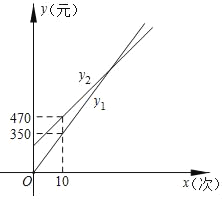
(1)按![]() 种方案购票,每张门票价格为 元;
种方案购票,每张门票价格为 元;
(2)按![]() 种方案购票,求
种方案购票,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)如果小颖假期30天,每天都到游泳馆游泳一次,通过计算她选择哪种购票方案比较合算.
查看答案和解析>>
科目: 来源: 题型:
【题目】某班数学活动小组测量吉林市“世纪之舟”的高度.他们制定了测量方案,并利用课余时间完成了实地测景,测量项目及数据如下表:
项目 | 内容 | |||
课题 | 测量吉林市“实际之舟”的高度 | |||
示意图 |
| 如图,用测角仪在 | ||
测量数据 |
|
|
| 测角仪 |
|
| 50米 | 1.5米 | |
… | … | |||
请你根据活动小组测得的数据,求世纪之舟的高![]() (结果保留小数点后一位).
(结果保留小数点后一位).
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】小明解方程![]() 出现了错误,解答过程如下:
出现了错误,解答过程如下:
方程两边都乘以![]() ,得
,得![]() (第一步)
(第一步)
去括号,得![]() (第二步)
(第二步)
移项,合并同类项,得![]() (第三步)
(第三步)
解得![]() (第四步)
(第四步)
![]() 原方程的解为
原方程的解为![]() (第五步)
(第五步)
(1)小明解答过程是从第_____步开始出错的,这一步正确的解答结果_____,此步的根据是_____.
(2)小明的解答过程缺少_____步骤,此方程的解为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,三张“黑桃”扑克牌,背面完全相同将三张扑克牌背面朝上,洗匀后放在桌面上甲,乙两人进行摸牌游戏,甲先从中随机抽取一张,记下数字再放回洗匀,乙再从中随机抽取一张.

(1)甲抽到“黑桃”,这一事件是 事件(填“不可能“,“随机“,“必然”);
(2)利用树状图或列表的方法,求甲乙两人抽到同一张扑克牌的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选择:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其他),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):


根据以上信息解答下列问题:
⑴ 这次被调查的学生有多少人?
⑵ 表中m的值为 ,并补全条形统计图;
⑶若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0),与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点P(m,0)(0<m<4),过点P作x轴的垂线交直线AB于点N,交抛物线于点M.

(1)求抛物线的解析式;
(2)若PN:PM=1:4,求m的值;
(3)如图2,在(2)的条件下,设动点P对应的位置是P1,将线段OP1绕点O逆时针旋转得到OP2,旋转角为α(0°<α<90°),连接AP2、BP2,求AP2+![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com