
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,AC=BC,点D是AC延长线上一点,连结BD.将
,AC=BC,点D是AC延长线上一点,连结BD.将![]() 绕着点C顺时针旋转90°得到
绕着点C顺时针旋转90°得到![]() ,延长AE交BD于F.
,延长AE交BD于F.
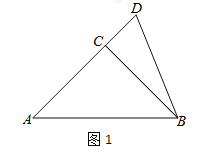
(1)依据题意补全图1;
(2)判断AE与BD的位置关系,说明理由;
(3)连结CF,求![]() 的度数.
的度数.
要想求出![]() 的度数,小明经过思考,得到了以下几种想法:
的度数,小明经过思考,得到了以下几种想法:
想法1:在AF上取一点G,使得AG=BF,需要先证明![]() ,然后再证明
,然后再证明![]() 是等腰直角三角形.
是等腰直角三角形.
想法2:取AB的中点O,连接OC,OF,只需要利用圆的性质证明![]() .
.
想法3:将![]() 绕点C逆时针旋转90°,得到
绕点C逆时针旋转90°,得到![]() ,只需证明
,只需证明![]() 是等腰直角三角形.
是等腰直角三角形.
请你参考上面的想法,帮助小明求解.(写出一种方法即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:直线l过点(0,2),且与x轴平行;直线![]() 与y轴交于A点,与直线l交于B点;抛物线
与y轴交于A点,与直线l交于B点;抛物线![]() 的顶点为C.
的顶点为C.
(1)求A,B两点的坐标;
(2)求点C的坐标(用m表示);
(3)若抛物线![]() 与线段AB有公共点,求m的取值范围.
与线段AB有公共点,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
下面是小东的探究过程,请补充完成:
(1)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(2)在平面直角坐标系xOy中描出了图象上的一些点,请你画出函数的图象;
下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 | 1.4 | 2.4 | 2.5 | 3 | 4 | 5 | … |
y | … | ﹣3.25 | ﹣2.33 | ﹣1.50 | ﹣1 | ﹣1.27 | 3.9 | 3.5 | 3 | m | 4.33 | … |
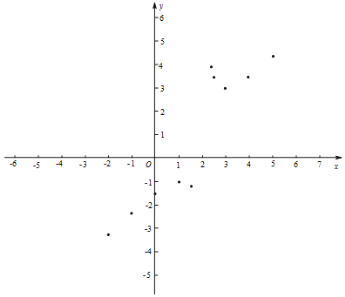
(3)求m的值;
(4)根据图象写出此函数的一条性质.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是![]() 的直径,C点在
的直径,C点在![]() 上,连接AC,
上,连接AC,![]() 的平分线交
的平分线交![]() 于点D,过点D作
于点D,过点D作![]() 交AC的延长线于点E.
交AC的延长线于点E.
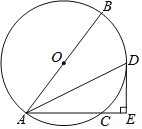
(1)求证:DE是![]() 的切线;
的切线;
(2)若AB=10,![]() ,连接CD,求CD的长.
,连接CD,求CD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
延庆是全市唯一一个全境域都是水源保护地的区域,森林覆盖率达到57.46%,“干净指数”连续五年全市第一,人均公共绿地面积41.88平方米,空气质量长期保持全市前列.根据区环保局的空气质量的通报,2012年空气质量为优,成为北京市最宜居的地方.
由于经济发展,私家车剧增等原因,2013年空气质量下降为良,尤其是PM2.5平均浓度有所增长,2013年PM2.5平均浓度约为78微克/立方米,比2012年PM2.5平均浓度增长了12.2%.延庆区作为2019年世园会和2022年冬奥会比赛的举办地,将全面治理“煤、气、尘”,逐渐降低PM2.5浓度,力争到2020年降至46微克/立方米,实现“延庆蓝”.
据悉,延庆将大力推广地源热泵、风能、太阳能等新能源和可再生能源.同时强化大货车监管,提升新能源车辆利用率.2020年新能源和可再生能源在延庆的使用比例将达到40%,煤炭能源消费总量占比3%以下,基本建成“无煤区”.
经过全面治理,2014年PM2.5平均浓度约为70微克/立方米,比2013年平均浓度降低了10.26%;2015年PM2.5平均浓度比2014年平均浓度降低了10%,为全市最低;2016年PM2.5平均浓度约为56微克/立方米.
根据以上材料解答下列问题:
(1)2015年PM2.5平均浓度约为 微克/立方米;
(2)选择统计表或统计图,将2013﹣2016年PM2.5平均浓度整理出来;
(3)根据上述材料和绘制的统计表或统计图中提供的信息,预估2017年的PM2.5平均浓度约为 微克/立方米;你的预估理由是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
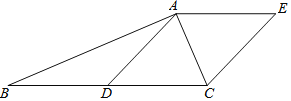
(1)求证:四边形ADCE是菱形;
(2)如果![]() ,
,![]() ,写出求菱形ADCE的面积的思路.
,写出求菱形ADCE的面积的思路.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是课本中“作一个角等于已知角”的尺规作图过程.
已知:∠AOB.
求作:一个角,使它等于∠AOB.
作法:如图
(1)作射线O'A';
(2)以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
(3)以O'为圆心,OC为半径作弧C'E',交O'A'于C';
(4)以C'为圆心,CD为半径作弧,交弧C'E'于D';
(5)过点D'作射线O'B'.
则∠A'O'B'就是所求作的角.
请回答:该作图的依据是_____.
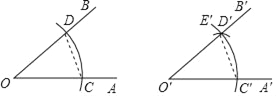
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两名队员参加射击训练,每人射击10次;根据两人成绩的信息,绘制了统计图,如图所示:
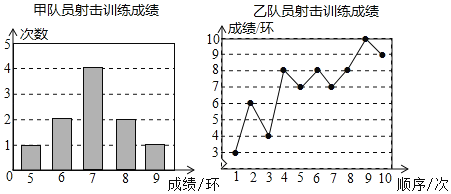
下面有四个推断:
①甲和乙成绩的众数不相同 ②甲和乙成绩的中位数相同
③甲和乙成绩的平均数不相同 ④甲的成绩比乙的成绩稳定
其中合理的是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于双曲线
中,对于双曲线![]() 和双曲线
和双曲线![]() ,如果
,如果![]() ,则称双曲线
,则称双曲线![]() 和双曲线
和双曲线![]() 为“倍半双曲线”,双曲线
为“倍半双曲线”,双曲线![]() 是双曲线
是双曲线![]() 的“倍双曲线”,双曲线
的“倍双曲线”,双曲线![]() 是双曲线
是双曲线![]() 的“半双曲线”,
的“半双曲线”,

(1)请你写出双曲线![]() 的“倍双曲线”是_____;双曲线
的“倍双曲线”是_____;双曲线![]() 的“半双曲线”是______;
的“半双曲线”是______;
(2)如图1,在平面直角坐标系![]() 中,已知点
中,已知点![]() 是双曲线
是双曲线![]() 在第一象限内任意一点,过点
在第一象限内任意一点,过点![]() 与
与![]() 轴平行的直线交双曲线
轴平行的直线交双曲线![]() 的“半双曲线”于点
的“半双曲线”于点![]() ,求
,求![]() 的面积;
的面积;
(3)如图2,已知点![]() 是双曲线
是双曲线![]() 在第一象限内任意一点,过点
在第一象限内任意一点,过点![]() 与
与![]() 轴平行的直线交双曲线
轴平行的直线交双曲线![]() 的“半双曲线”于点
的“半双曲线”于点![]() ,过点
,过点![]() 与
与![]() 轴平行的直线交双曲线
轴平行的直线交双曲线![]() 的“半双曲线”于点
的“半双曲线”于点![]() ,若
,若![]() 的面积记为
的面积记为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
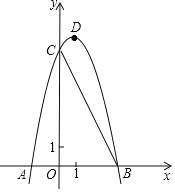
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点,![]() .
.
(1)求抛物线的表达式及其顶点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,将抛物线沿其对称轴向上平移
,将抛物线沿其对称轴向上平移![]() 个单位,使抛物线与线段
个单位,使抛物线与线段![]() (含线段端点)只有1个公共点.求
(含线段端点)只有1个公共点.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com