
科目: 来源: 题型:
【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D-d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
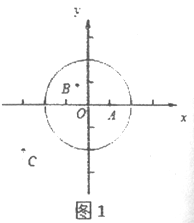
A(1,0)的距离跨度______________;
B(-![]() ,
, ![]() )的距离跨度____________;
)的距离跨度____________;
C(-3,-2)的距离跨度____________;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是______________.
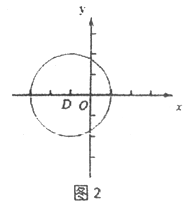
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(-1,0)为圆心,2为半径的圆,直线y=k(x-1)上存在到G2的距离跨度为2的点,求k的取值范围.
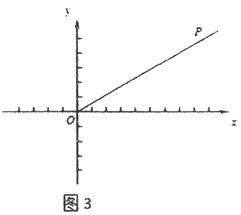
(3)如图3,在平面直角坐标系xOy中,射线OP:y=![]() x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+l与双曲线y=![]() 的一个交点为A(m,-3).
的一个交点为A(m,-3).
(1)求双曲线的表达式;
(2)过动点P(n,0)(n<0)且垂直于x轴的直线与直线y=2x+l和双曲线y=![]() 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断:
①甲种作物受环境影响最小;②乙种作物平均成活率最高;
③丙种作物最适合播种在山腰;
④如果每种作物只能在一个地方播种,那么山脚,山腰和山顶分别播种甲,乙,丙三种作物能使得成活率最高.其中合理的是( )

A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,对“隔离直线”给出如下定义:
点P(x,m)是图形G1上的任意一点,点Q(x,n)是图形G2上的任意一点,若存在直线l:kx+b(k≠0)满足m≤kx+b且n≥kx+b,则称直线l:y=kx+b(k≠0)是图形G1与G2的“隔离直线”.
如图,直线l:y=-x-4是函数y=![]() (x<0)的图象与正方形OABC的一条“隔离直线”.
(x<0)的图象与正方形OABC的一条“隔离直线”.
(1)在直线y1=-2x,y2=3x+1,y3=-x+3中,是如图函数y=![]() (x<0)的图象与正方形OABC的“隔离直线”的为y1=-2x;
(x<0)的图象与正方形OABC的“隔离直线”的为y1=-2x;
请你再写出一条符合题意的不同的“隔离直线”的表达式:y=-3x;
(2)如图,第一象限的等腰直角三角形EDF的两腰分别与坐标轴平行,直角顶点D的坐标是(![]() ,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
(3)正方形A1B1C1D1的一边在y轴上,其它三边都在y轴的右侧,点M(1,t)是此正方形的中心.若存在直线y=2x+b是函数y=x2-2x-3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”,请直接写出t的取值范围.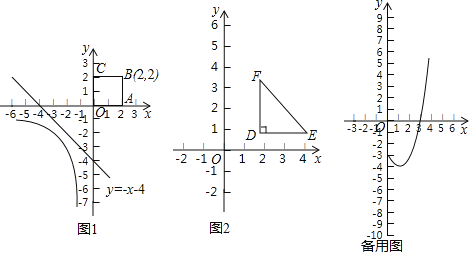
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(与点
上的动点(与点![]() 不重合),连接
不重合),连接![]() .
.
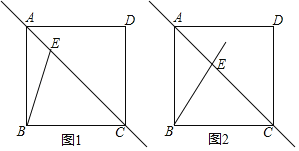
(1)将射线![]() 绕点
绕点![]() 顺时针旋转45°,交直线
顺时针旋转45°,交直线![]() 于点
于点![]() .
.
①依题意补全图1;
②小研通过观察、实验,发现线段![]() ,
,![]() ,
,![]() 存在以下数量关系:
存在以下数量关系:
![]() 与
与![]() 的平方和等于
的平方和等于![]() 的平方.小研把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:
的平方.小研把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:
想法1:将线段![]() 绕点
绕点![]() 逆时针旋转90°,得到线段
逆时针旋转90°,得到线段![]() ,要证
,要证![]() 的关系,只需证
的关系,只需证![]() 的关系.
的关系.
想法2:将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,要证
,要证![]() 的关系,只需证
的关系,只需证![]() 的关系.
的关系.
…
请你参考上面的想法,用等式表示线段![]() 的数量关系并证明;(一种方法即可)
的数量关系并证明;(一种方法即可)
(2)如图2,若将直线![]() 绕点
绕点![]() 顺时针旋转135°,交直线
顺时针旋转135°,交直线![]() 于点
于点![]() .小研完成作图后,发现直线
.小研完成作图后,发现直线![]() 上存在三条线段(不添加辅助线)满足:其中两条线段的平方和等于第三条线段的平方,请直接用等式表示这三条线段的数量关系.
上存在三条线段(不添加辅助线)满足:其中两条线段的平方和等于第三条线段的平方,请直接用等式表示这三条线段的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形![]() 为凹四边形.
为凹四边形.
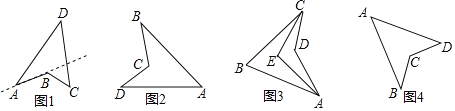
(2)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形![]() 是凹四边形.
是凹四边形.
求证:![]() .
.
(3)性质应用:
如图3,在凹四边形![]() 中,
中,![]() 的角平分线与
的角平分线与![]() 的角平分线交于点
的角平分线交于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() °.
°.
(4)类比学习:
如图4,在凹四边形![]() 中,点
中,点![]() 分别是边
分别是边![]() 的中点,顺次连接各边中点得到四边形
的中点,顺次连接各边中点得到四边形![]() .若
.若![]() ,则四边形
,则四边形![]() 是 .(填写序号即可)
是 .(填写序号即可)
A.梯形 B.菱形 C.矩形 D.正方形.
查看答案和解析>>
科目: 来源: 题型:
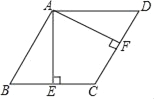
【题目】如图,在ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.
(1)求证:四边形ABCD是菱形;
(2)若∠EAF=60°,CF=2,求AF的长.
查看答案和解析>>
科目: 来源: 题型:
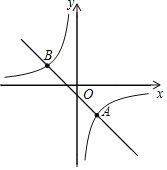
【题目】如图,在平面直角坐标系xOy中,已知直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(2,-3)和点B(n,2);
(m≠0)交于点A(2,-3)和点B(n,2);
(1)求直线与双曲线的表达式;
(2)点P是双曲线y=![]() (m≠0)上的点,其横、纵坐标都是整数,过点P作x轴的垂线,交直线AB于点Q,当点P位于点Q下方时,请直接写出点P的坐标.
(m≠0)上的点,其横、纵坐标都是整数,过点P作x轴的垂线,交直线AB于点Q,当点P位于点Q下方时,请直接写出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:![]() ),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
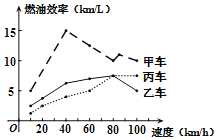
A.当行驶速度为![]() 时,每消耗1升汽油,甲车能行驶
时,每消耗1升汽油,甲车能行驶![]()
B.消耗1升汽油,丙车最多可行驶![]()
C.当行驶速度为![]() 时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同
时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同
D.当行驶速度为![]() 时,若行驶相同的路程,丙车消耗的汽油最少
时,若行驶相同的路程,丙车消耗的汽油最少
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() ;直线
;直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是第一象限内抛物线上一动点.
是第一象限内抛物线上一动点.
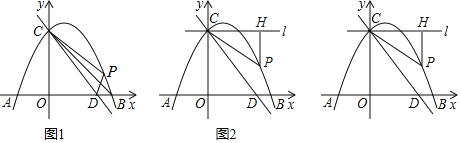
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)如图2,过点![]() 作直线
作直线![]() 轴,过点
轴,过点![]() 作
作![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 的对应点
的对应点![]() 恰好落在直线
恰好落在直线![]() 上,同时使点
上,同时使点![]() 的对应点
的对应点![]() 恰好落在坐标轴上,请直接写出此时点
恰好落在坐标轴上,请直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com