
科目: 来源: 题型:
【题目】对于平面直角坐标系xOy中的两个图形M和N,给出如下定义:若在图形M上存在一点A,图形N上存在两点B,C,使得△ABC是以BC为斜边且BC=2的等腰直角三角形,则称图形M与图形N具有关系φ(M,N).
(1)若图形X为一个点,图形Y为直线y=x,图形X与图形Y具有关系φ(X,Y),则点![]() ,P2(1,1),P3(2,﹣2)中可以是图形X的是 ;
,P2(1,1),P3(2,﹣2)中可以是图形X的是 ;
(2)已知点P(2,0),点Q(0,2),记线段PQ为图形X.
①当图形Y为直线y=x时,判断图形X与图形Y是否既具有关系φ(X,Y)又具有关系φ(Y,X),如果是,请分别求出图形X与图形Y中所有点A的坐标;如果不是,请说明理由;
②当图形Y为以T(t,0)为圆心,![]() 为半径的⊙T时,若图形X与图形Y具有关系φ(X,Y),求t的取值范围.
为半径的⊙T时,若图形X与图形Y具有关系φ(X,Y),求t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C:y=ax2﹣2ax+3与直线l:y=kx+b交于A,B两点,且点A在y轴上,点B在x轴的正半轴上.
(1)求点A的坐标;
(2)若a=﹣1,求直线l的解析式;
(3)若﹣3<k<﹣1,求a的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】某学校共有六个年级,每个年级10个班,每个班约40名同学.该校食堂共有10个窗口,中午所有同学都在食堂用餐.经了解,该校同学年龄分布在12岁(含12岁)到18岁(含18岁)之间,平均年龄约为15岁.小天、小东和小云三位同学,为了解全校同学对食堂各窗口餐食的喜爱情况,各自进行了抽样调查,并记录了相应同学的年龄,每人调查了60名同学,将收集到的数据进行了整理.小天从初一年级每个班随机抽取6名同学进行调查,绘制统计图表如下:

小东从全校每个班随机抽取1名同学进行调查,绘制统计图表如下:
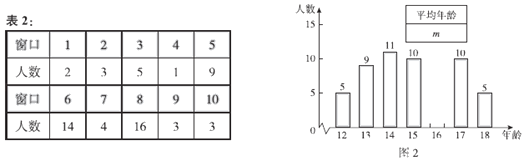
小云在食堂门口,对用餐后的同学采取每隔10人抽取1人进行调查,绘制统计图表如下:
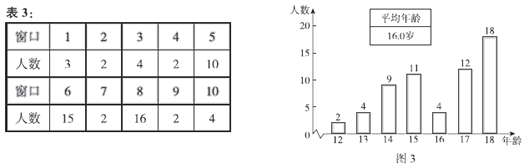
根据以上材料回答问题:
(1)写出图2中m的值,并补全图2;
(2)小天、小东和小云三人中,哪个同学抽样调查的数据能较好地反映出该校同学对各窗口餐食的喜爱情况,并简要说明其余同学调查的不足之处;
(3)为使每个同学在中午尽量吃到自己喜爱的餐食,学校餐食管理部门应为 窗口尽量多的分配工作人员,理由为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小宇从课本上研究函数的活动中获得启发,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小宇的探究过程,请补充完整:
(1)函![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)如图,在平面直角坐标系xOy中,完成以下作图步骤:
①画出函数![]() 和
和![]() 的图象;
的图象;
②在x轴上取一点P,过点P作x轴的垂线l,分别交函数![]() 和
和![]() 的图象于点M,N,记线段MN的中点为G;
的图象于点M,N,记线段MN的中点为G;
③在x轴正半轴上多次改变点P的位置,用②的方法得到相应的点G,把这些点用平滑的曲线连接起来,得到函数![]() 在y轴右侧的图象.继续在x轴负半轴上多次改变点P的位置,重复上述操作得到该函数在y轴左侧的图象.
在y轴右侧的图象.继续在x轴负半轴上多次改变点P的位置,重复上述操作得到该函数在y轴左侧的图象.
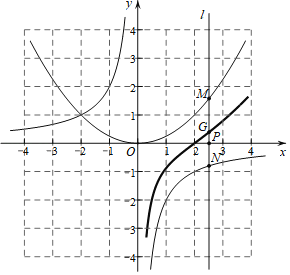
(3)结合函数![]() 的图象,发现:
的图象,发现:
①该函数图象在第二象限内存在最低点,该点的横坐标约为(保留小数点后一位);
②该函数还具有的性质为: (一条即可).
查看答案和解析>>
科目: 来源: 题型:
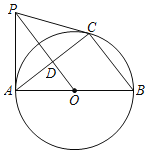
【题目】如图,AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,连接AC,BC,OP,AC与OP相交于点D.
(1)求证:∠B+∠CPO=90°;
(2)连结BP,若AC=![]() ,sin∠CPO=
,sin∠CPO=![]() ,求BP的长.
,求BP的长.
查看答案和解析>>
科目: 来源: 题型:
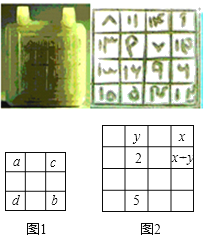
【题目】如图是在浦东陆家嘴明代陆深古墓中发掘出来的宝玉﹣﹣明白玉幻方.其背面有方框四行十六格,为四阶幻方(从1到16,一共十六个数目,它们的纵列、横行与两条对角线上4个数相加之和均为34).小明探究后发现,这个四阶幻方中的数满足下面规律:在四阶幻方中,当数a,b,c,d有如图1的位置关系时,均有a+b=c+d=17.如图2,已知此幻方中的一些数,则x的值为__.
查看答案和解析>>
科目: 来源: 题型:
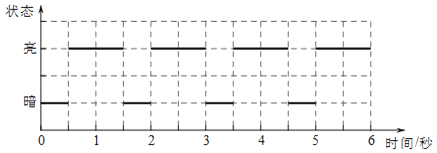
【题目】按《航空障碍灯(MH/T6012﹣1999)》的要求,为保障飞机夜间飞行的安全,在高度为45米至105米的建筑上必须安装中光强航空障碍灯(AviationObstructionlight).中光强航空障碍灯是以规律性的固定模式闪光.在下图中你可以看到某一种中光强航空障碍灯的闪光模式,灯的亮暗呈规律性交替变化,那么在一个连续的10秒内,该航空障碍灯处于亮的状态的时间总和最长可达__秒.
查看答案和解析>>
科目: 来源: 题型:
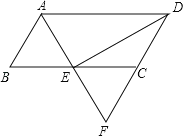
【题目】如图,在ABCD中,∠BAD的角平分线交BC于点E,交DC的延长线于点F,连接DE.
(1)求证:DA=DF;
(2)若∠ADE=∠CDE=30°,DE=2![]() ,求ABCD的面积.
,求ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小宇设计的“作已知直角三角形的中位线”的尺规作图过程.
已知:在△ABC中,∠C=90°.
求作:△ABC的中位线DE,使点D在AB上,点E在AC上.
作法:如图,
①分别以A,C为圆心,大于![]() AC长为半径画弧,两弧交于P,Q两点;
AC长为半径画弧,两弧交于P,Q两点;
②作直线PQ,与AB交于点D,与AC交于点E.
所以线段DE就是所求作的中位线.
根据小宇设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接PA,PC,QA,QC,DC,
∵PA=PC,QA= ,
∴PQ是AC的垂直平分线( )(填推理的依据).
∴E为AC中点,AD=DC.
∴∠DAC=∠DCA,
又在Rt△ABC中,有∠BAC+∠ABC=90°,∠DCA+∠DCB=90°.
∴∠ABC=∠DCB( )(填推理的依据).
∴DB=DC.
∴AD=BD=DC.
∴D为AB中点.
∴DE是△ABC的中位线.

查看答案和解析>>
科目: 来源: 题型:
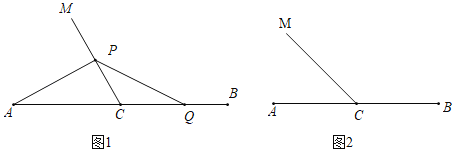
【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com