
科目: 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目: 来源: 题型:
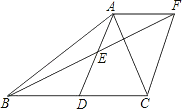
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,且AF=DC,连接CF.
(1)求证:D是BC的中点;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形A0B0C0A1的边长为1,正方形A1B1C1A2的边长为2,正方形A2B2C2A3的边长为4,正方形A3B3C3A4的边长为8……依此规律继续作正方形AnBnnAn+1,且点A0,A1,A2,A3,…,An+1在同一条直线上,连接A0C1交A1B1于点D1,连接A1C2交A2B2于点D2,连接A2C3交A3B3于点D3……记四边形A0B0C0D1的面积为S1,四边形A1B1C1D2的面积为S2,四边形A2B2C2D3的面积为S3……四边形An﹣1Bn﹣1Cn﹣1Dn的面积为Sn,则S2019=_____.

查看答案和解析>>
科目: 来源: 题型:
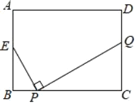
【题目】如图,矩形ABCD中,AB=6,BC=8,E为AB的中点,P为BC上一动点,作PQ⊥EP交直线CD于点Q,设点P每秒以1个单位长度的速度从点B运动到点C停止,在此时间段内,点Q运动的平均速度为每秒_____个单位.
查看答案和解析>>
科目: 来源: 题型:
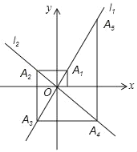
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…,依次进行下去,则点A2019的坐标为( )
A.(21009,21010)B.(﹣21009,21010)
C.(21009,﹣21010)D.(﹣21009,﹣21010)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,
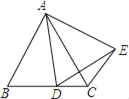
(1)求证:△ABD≌△ACE;
(2)若CE=![]() ,求△ACD的面积;
,求△ACD的面积;
(3)若△ACE是直角三角形,则BD的长是 (直接写出答案).
查看答案和解析>>
科目: 来源: 题型:
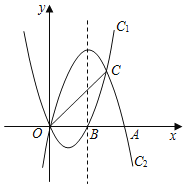
【题目】如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
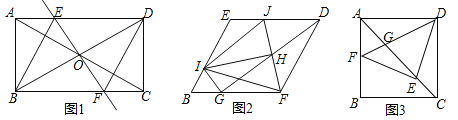
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com