
科目: 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,四边形ABCD是平行四边形;
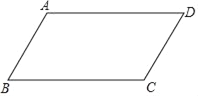
求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(1)连接AC;
(2)作AC的垂直平分线EF分别交BC,AD于E,F.
(3)连接AE,CF
所以四边形AECF是菱形.

老师说:“小凯的作法正确”.
回答下列问题:
根据小凯的做法,小明将题目改编为一道证明题,请你帮助小明完成下列步骤:
(1)已知:在平行四边形ABCD中,点E、F分别在边BC、AD上, .(补全已知条件)
求证:四边形AECF是菱形.
(2)证明:(写出证明过程)
查看答案和解析>>
科目: 来源: 题型:
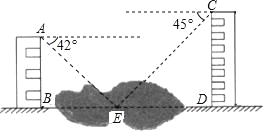
【题目】如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m.AB和CD之间有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上.求两幢建筑物之间的距离BD.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,0),B(0,﹣2),C(2,﹣1);
(1)画出关于x轴对称的△AB1C1;
(2)以原点O为位似中心,画出△A2B2C2,使△A2B2C2与△ABC的位似比为2:1.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知在平面直角坐标系中,等边△ABC的顶点A、B、C的坐标分别为(a,4)、(b,0)、(c,6),且a<b<c,则等边△ABC的边长为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的( )
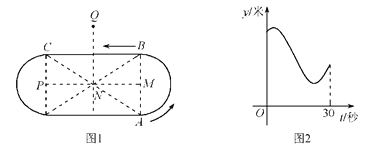
A. 点M B. 点N C. 点P D. 点Q
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,直线y=![]() x﹣2与x轴交于点B,与y轴交于点C,二次函数y=
x﹣2与x轴交于点B,与y轴交于点C,二次函数y=![]() x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
(1)求二次函数的解析式;
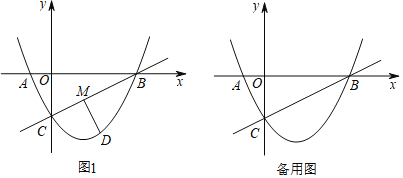
(2)如图1,点M是线段BC上的一动点,动点D在直线BC下方的二次函数图象上.设点D的横坐标为m.
①过点D作DM⊥BC于点M,求线段DM关于m的函数关系式,并求线段DM的最大值;
②若△CDM为等腰直角三角形,直接写出点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=8,AB=10,D,E两点分别是AC,CB上的点,且CD=6,DE∥AB,将△CDE绕点C顺时针旋转一周,记旋转角为α.
(1)问题发现
①当α=0°时,![]() = ;
= ;
②当α=90°时,![]() = .
= .
(2)拓展探究
请你猜想当△CDE在旋转的过程中,![]() 是否发生变化?根据图2证明你的猜想.
是否发生变化?根据图2证明你的猜想.
(3)问题解决
在将△CDE绕点C顺时针旋转一周的过程中,当AD=2![]() 时,BE= ,此时α= .
时,BE= ,此时α= .

查看答案和解析>>
科目: 来源: 题型:
【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加,某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见表:
A型销售数量(台) | B型销售数量(台) | 总利润(元) |
5 | 3 | 950 |
3 | 4 | 900 |
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共80台,其中B型空气净化器的进货量不多于A型空气净化器的2倍,为使该公司销售完这80台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为200m3/小时,B型空气净化器的净化能力为300m3/小时,某长方体室内活动场地的总面积为200m2,室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,若不考虑空气对流等因素,至多要购买A型空气净化器多少台?
查看答案和解析>>
科目: 来源: 题型:
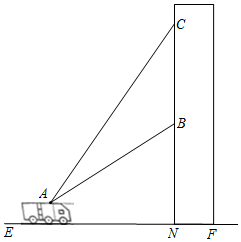
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABDC的顶点D,C在反比例函数y=![]() 上(k>0,x>0),横坐标分别为
上(k>0,x>0),横坐标分别为![]() 和2,对角线BC∥x轴,菱形ABDC的面积为9.
和2,对角线BC∥x轴,菱形ABDC的面积为9.
(1)求k的值及直线CD的解析式;
(2)连接OD,OC,求△OCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com