
科目: 来源: 题型:
【题目】如图,在△ABC中,点D在边AB上,点E在边AC上,CE=BD,连接CD,BE,BE与CD相交于点F.
(1)如图1,若△ACD为等边三角形,且CE=DF,求∠CEF的度数;
(2)如图2,若AC=AD,求证:EF=FB;
(3)如图3,在(2)的条件下,若∠CFE=45°,△BCD的面积为4,求线段CD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 在
在![]() 轴的负半轴上,顶点
轴的负半轴上,顶点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() ,线段
,线段![]() 的垂直平分线分别交
的垂直平分线分别交![]() 于点
于点![]() .
.
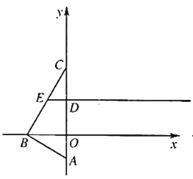
(1)点![]() 的坐标;
的坐标;
(2)点![]() 为线段
为线段![]() 的延长线上的一点,连接
的延长线上的一点,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,点![]() 为线段
为线段![]() 的延长线上一点,连接
的延长线上一点,连接![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区有一块长方形水稻试验田,试验田的长、宽(如图所示,长度单位:米),试验田分两部分,一部分为水渠,另一部分为新型水稻种植田(阴影部分).
(1)用含a,b的式子表示新型水稻种植田的面积是多少平方米(结果化成最简形式);
(2)若a=30,b=40,在“农民丰收节”到来之时水稻成熟,计划先由甲型收割机收割一部分,再由乙型收割机收割剩余部分,甲型收割机收割水稻每平方米的费用为0.3元,乙型收割机收割水稻每平方米的费用为0.5元,若要收割全部水稻的费用不超过5000元,问甲型收割机最少收割多少平方米的水稻?

查看答案和解析>>
科目: 来源: 题型:
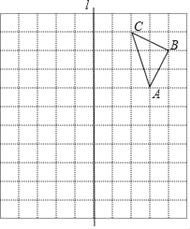
【题目】如图,直线l与△ABC在边长为1个单位长度的小正方形网格中,点A,B,C都为网格线的交点.
(1)请画出△ABC关于直线l对称的△A1B1C1(点A,B,C的对称点分别为A1,B1,C1).
(2)请画出将线段AC向左平移3个单位,再向下平移5个单位得到的线段A2C2(点A,C的对应点分别为A2,C2),再以A2C2为斜边画一个等腰直角三角形A2B2C2.
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图: A,B产品单价变化统计表
第一次 | 第二次 | 第三次 | |
A产品单价 (元/件) | 6 | 5.2 | 6.5 |
B产品单价 (元/件) | 3.5 | 4 | 3 |

并求得了A产品三次单价的平均数和方差:![]() ;
;![]()
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0)使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.

(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
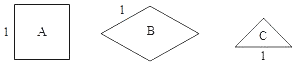
【题目】将图中的![]() 型(正方形)、
型(正方形)、![]() 型(菱形)、
型(菱形)、![]() 型(等腰直角三角形)纸片分别放在
型(等腰直角三角形)纸片分别放在![]() 个盒子中,盒子的形状、大小、质地都相同,再将这
个盒子中,盒子的形状、大小、质地都相同,再将这![]() 个盒子装入一只不透明的袋子中.
个盒子装入一只不透明的袋子中.
(1)搅匀后从中摸出![]() 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
(2)搅匀后先从中摸出![]() 个盒子(不放回),再从余下的
个盒子(不放回),再从余下的![]() 个盒子中摸出
个盒子中摸出![]() 个盒子,把摸出的
个盒子,把摸出的![]() 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
查看答案和解析>>
科目: 来源: 题型:
【题目】为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释效过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
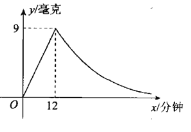
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com