
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,OB=OC=2,AB=![]() .
.
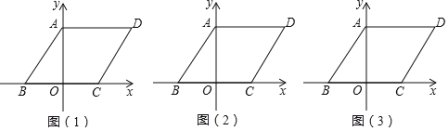
(1)求点D的坐标,直线CD的函数表达式;
(2)已知点P是直线CD上一点,当点P满足S△PAO=![]() S△ABO时,求点P的坐标;
S△ABO时,求点P的坐标;
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F(不与A、B重合),使以A、 C、 F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,AB=4.若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合).

(1)求证:△ABE∽△DCA;
(2)若BE·CD=k(k为常数),求k的值;
(3)在旋转过程中,当△AFG旋转到如图2的位置时,AG与BC交于点E,AF的延长线与CB的延长线交于点D,那么(2)中k的值是否发生了变化?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店准备进一批季节性小家电,进价为每台40元,经市场预测,售价为每台48元时,可售出220台;售价每增加1元,销售量减少10台。
(1)当售价为55元,销售量为多少台?
(2)因受库存的影响,每批次进货个数不得超过160台,若商店想获得2000元利润,则应进货多少台?售价定为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形.

查看答案和解析>>
科目: 来源: 题型:
【题目】小明、小亮两人用如图所示的两个分隔均匀的转盘做游戏:分别转动两个转盘,转盘停止后,将两个指针所指数字相加(若指针恰好停在分割线上,则重转一次).如果这两个数字之和小于8(不包括8),则小明获胜;否则小亮获胜。
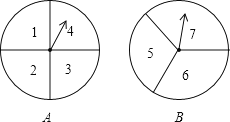
(1)利用列表法或画树状图的方法表示游戏所有可能出现的结果;
(2)这个游戏对双方公平吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,0),B(0,2),C(2,1);

(1)以原点O为位似中心,在第二象限画出△A1B1C1,使△A1B1C1与△ABC的位似比为2:1;
(2)点P(a,b)为线段AC上的任意一点,则点P在△A1B1C1中的对应点P1的坐标为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,交AB于N.下列结论:①DE=CN;②![]() ;③S△DEC=3S△BNH;④∠BGN=45°;⑤
;③S△DEC=3S△BNH;④∠BGN=45°;⑤![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
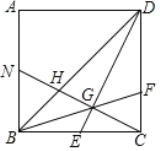
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目: 来源: 题型:
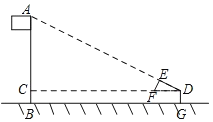
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5m,EF=0.25m,目测点D到地面的距离DG=1.5m,到旗杆的水平距离DC=20m,则旗杆的高度为( )
A.![]() mB.
mB.![]() m
m
C.11.5mD.10m
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,连接MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )
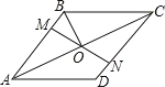
A.28°B.56°C.62°D.72°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com